Chapter 1: Mathematical Proof Energy has been Misdefined in Physics Chapter Summary Energy is defined as that which is conserved during transformation into other forms of energy. Before the concept of energy existed, researchers found that mass times velocity was a conserved quantity of motion (c. 1635). In 1686, Gottfried Leibniz claimed to show that it is mass times velocity squared which is the conserved quantity of motion, and it has since become the definition of kinetic energy. The mathematics of rockets can now be used to show that Leibniz was wrong; it is really the original concept, mass time velocity, which is the quantity conserved for transformations of kinetic energy. About ninety percent of physics is corrupted by the error. A uniformly applied error is useful for engineering, but not science. Physics only functions as super-engineering, not real science. ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ The Results Show This: Energy is defined as "that which is conserved during transformations." Conserved means totals stay the same when components are re-arranged. So the test for the definition of kinetic energy is to re-arrange the components and see which total stays the same. Part 1: Kinetic energy is not ½mv². Rocket burn time: Therefore, both masses do not have the same energy; the rocket does not transform energy in proportion to ½mv²; ½mv² is not kinetic energy; and a gallon of fuel does not produce a consistent amount of ½mv². Part 2: Kinetic energy is mv. Rocket burn time: Therefore, both masses have the same amount of energy; the rocket transforms energy in proportion to mv; mv is kinetic energy; and a gallon of fuel produces a consistent amount of mv. The proof that there are no errors in the math is that the ratio for the first two tests is 2.00000000000000, while the ratio of the second two tests is 1.00000000000000. Any error would replace the zeros with other numbers. All logic and evidence of energy point to the same conclusion. The logic created the need to derive the mathematical proof. About ninety percent of physics is corrupted by the error. Physicists mindlessly assume the discrepancies can be accounted for in the exhaust of the rocket. There's no question where the energy is located. It's a question of defining energy in terms of transformation instead of nonsensical math. With ½mv², energy addition (including transformation) varies with reference frames, while addition of mv is independent of reference frames. Key Point With rocket math, the analysis is referenced to the combustion chamber, where equal and opposite forces determine the result. The reference point is where the force acts. Everywhere else, energy is defined relative to the starting point or some similar, external reference frame. When the reference is the point where the force acts, you get the correct definition of energy, which is momentum. When the reference point is anyplace else, you get the incorrect definition of energy, which is ½mv². This is because the incorrect definition of energy is equal to force times distance for an accelerating mass. Distance references to something other than the point were the force acts. History There has not been an iota of physics since Newton’s laws which has not been grossly in error. Newton’s laws were published in 1687. A year earlier the incorrect definition of kinetic energy was published by Gottfried Leibniz. Early in the century, scientists were studying motion through the use of pendulums, because the velocity of a mass could be determined from the height of the swing. Masses were allowed to collide on a pendulum to determine the transfer of velocities. It was noticed that both mass times velocity (mv) and mass times velocity squared (mv²) were conserved through the interactions. Conserved means the same totals were found after the interactions as before. Mass times velocity squared was ignored as an artifact, since nothing can move at velocity squared. Its motion is its velocity, not velocity squared. Sometime around 1635 René Descartes published a summary saying there is a fixed amount of motion in the universe, because it is conserved through interactions. By motion, he meant mass times velocity (mv). Leibniz gave no justification for his starting point. The starting point could be modified to relate to time instead of distance saying that if a four kilogram object is dropped for one second, it will do the same thing as a one kilogram object dropped for four seconds. These relationships conserve mass times velocity but not mass times velocity squared. Force times time is proportional to mass times velocity nonsquared. This issue was argued for two hundred years and then decided in Leibniz’s favor due to experiments by James Joule in stirring water in a wooden bucket to determine the relationship between force and heat. Mass times velocity squared (mv²) became the definition for kinetic energy. But mass times velocity non squared (mv) was not totally discarded. It was assumed to be conserved in the absence of added energy and was referred to as momentum. I noticed something wrong in 1983 reading an article in Science Digest, where astronomers said they observed masses flying out of quasars at ten times the velocity of light. Other physicists said the result must have been an optical illusion, since relativity says nothing can move faster than the speed of light. It raised the question of the validity of relativity. Why did Einstein square the velocity of light in his equation E=mc², when nothing can move at velocity squared. He obviously paralleled the definition of kinetic energy, but why was velocity squared in it? The reason was because it is equal to force times distance for an accelerating mass. But why is force times distance conserved? It’s not valid to conserve force times distance, because the force does not move through any distance relative to the mass it acts upon. The force moves with the mass. Distance relates to the starting point. The force does not act upon the starting point. Physicists turn green when you tell them that. They assume you can combine any factors any way possible, once facts have been proven. What is proof without proper logic? Physicists despise logic. They assume any mathematics which balances equations is a law of nature. I mailed a write-up to several physics labs explaining that rockets show that energy is proportional to force times time, not force times distance. Rockets burn energy at a constant rate and produce a constant force, which combines force and time independent of distance or motion. Distance is relative (undefined), but time is not. A rocket accelerating in space has a different velocity relative to each object which has a different velocity. Someone at the Jet Propulsion Laboratory responded saying I could prove the definition of kinetic energy to be correct by winding a tapered yoyo. They must have been calling me a yoyo, since the concept is ridiculous; so I wrote back explaining how the characteristics of rockets show the definition of energy to be wrong. In response, they sent me the basic rocket equations saying the equations balance, and therefore the definition of energy is correct. Balancing equations says nothing about correctness. But with the rocket equations, I could use rockets to replace gravity and show the misdefinition of energy. I have never seen the rocket equations in print. I think the reason why Wernher Von Braun was brought to the U.S. is because the Germans figured out how to balance the rocket equations, and the Americans couldn’t figure it out, because there is a small trick to it. The fuel used by a constant powered rocket is simply its burn time. Therefore, rocket burn time can replace gravity to determine the amount of energy in the falling objects upon which the definition of kinetic energy is based. The rocket is arbitrarily given three properties, and the rest is calculated. Its mass is 20kg; its rate of mass loss is 0.01kg/s; and the separation velocity of the exhaust is 1000m/s. mass ratio averaged for loss of mass = Example: Constant C in burn time: Total Time of Burn: Fraction for Payload: Explanation: Numbers for each object: Time Dropping: A: t = [2(1m)/9.81]½ = 0.45152364098573 sec Velocity Dropping: A: v = 9.81(0.45152364098573) = 4.42944691807002 m/s Constant C in burn time: velocity of rocket = A: c = 103ln[100(24)] = 7783.22401633603 Total Time of Burn: t = mo/0.01 - [(c-v)/103]ex A: 24kg/0.01 - [(7783.22401633603-4.42944691807002)/103]ex = 10.6071633272070 sec Fraction for payload: A: c = 100(4kg)ln[100(24kg)] = 3113.28960653441 Time of Burn for Payload Only: A: t = -100(4kg)ln[100(24kg) - 10.6071633272070] + 3113.28960653441 = 1.77177876722800 sec Ratios: A second proof is that power gets absurd at the high velocity of a rocket. The erroneous definition of energy has a velocity problem. First, squaring velocity creates a problem in the kinetic energy formula (½mv²). Then power becomes absurd at high velocities.
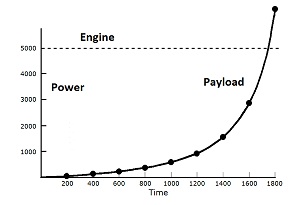
Power of rocket payload as rate of change in ½mv²
The horizontal line is the power of the rocket engine. Rockets are usually constant powered, meaning they use fuel at a constant rate. Power is rate of energy addition. Mathematically, the power of the rocket mass and exhaust mass are added to create the constant power. But there is a problem with that analysis. As velocity increases, it reaches a point where the power added to the payload is greater power than the engine produces. When the definition of energy is corrected, power is proportional to force only, which is constant, as fuel use is constant. Calculations mo = mass of rocket at start = 21kg mp = mass of payload = 1kg m' = rate of mass loss = -0.01kg/s mt = mass of rocket at time T = mo + m't ve = separation velocity of exhaust = 103m/s (pos) F = force = -m've = -(-0.01)(103) = 10 newtons v't = acceleration at time T = F/mt v = velocity = ∫v'dt = ∫10/(mo - 0.01t)dt = ∫103/(100mo - t)dt = -103ln(100mo - t) + c(-c is quantity at T = 0) c = 103ln(100mo) = 7650 Shortcut Formula for Velocity: Δv = veln(mo/mt) = (1000)ln(21/mt) With the existing (erroneous) definition of energy, power as rate of energy addition reduces to force times velocity. With simple math, the logic is this: ½mv²/t = ½m·v/t·v = ½mav = ½Fv. The one half is dropped, because it was for averaging. More precisely: the derivative of ½mv² with respect to t = ½m(v²)' + (m)'(½v²). KE'p = ½m(2vv') + 0(½v²) = mv'v = mav = Fv The force acting upon the payload (Fp) is the force of the engine (10 newtons) times the mass ratio (mp/mt). m = 21kg total, payload = 1kg
The Logic Problem The rocket engine produces power at 5,000 units, and in 1800 seconds, the payload is acquiring power at 6,487 units. The payload is acquiring power at a greater rate than the engine produces it; but the engine is the only source of power. This occurs because the erroneous definition of energy results in velocity being included as an element of power, when power should be proportional to force only. The reason why the rocket payload acquires energy as power at a higher rate than the power of the rocket engine is because velocity is an element of power, when energy is defined as ½mv². This means that the rocket engine creates velocity, and then velocity becomes a source of power. Velocity is not really a source of power. Yet the incorrect definition of energy makes it a source of power. The graph above shows why velocity should not be a source of power. When velocity increases, the total power for an object which does not lose mass, such as the rocket payload, gets larger than that produced by the real source of power—the engine. Joule's constant is the relationship between kinetic energy and heat. Kinetic energy is usually expressed as force times distance (Newton-meters), which physicists call work, but it is interchangeable with kinetic energy. The most recent value given is 4.1868 Newton-meters per calorie. Joule said it is 4.2 N-m/calorie, which means he was only off by 3 parts per thousand. Pretty good for 1845, huh. Except that only fakery produces that much perfection without real tools of science. Now days Joule's constant is usually called "the mechanical equivalent of heat." Physicists apparently don't want to draw too much attention to what occurred in 1845. Otherwise, they just love to name their numbers after some god. Physicists assume that Joule's constant shows that heat transforms into ½mv², not mv. There is no real Joule's constant. The number stems from illusion, as often occurs when allowing perception to contradict logic. James P. Joule supposedly measured the constant in 1845. In actuality, he did not have the slightest ability to make such a measurement. Joule claimed to have stirred water in a wooden bucket and measured the heat produced. The kinetic energy was said to be determined by weights which were dropped to turn a paddle in the water. There were no thermal constants at that time to determine where the heat was going. Joule was producing such a minuscule amount of heat that it would have dissipated into the environment in a few seconds, while he stirred the water for one or two hours. Yet his error was supposedly only a few parts per thousand (ppt). He did not describe the details in his brief publication. What he said was that he dropped the weights 12 yards (11m), rewinding and dropping them 16 times for each measurement of temperature. The temperature increase was 0.5°F or less. The weights were four pounds each, and two were used for balance. The rate of decent was said to be one foot per second. Joule was not a physicist. He mimicked what physicists were doing. When they ran into problems which they could not solve, Joule claimed to have a gimmick for solving them. To account for environmental influences, he dropped weights an extra time. Here's the way he said it: "A series of nine experiments were performed in the above manner, and nine experiments were made in order to eliminate the cooling or heating effects of the atmosphere." Nothing more. There was no way to account for environmental effects experimentally. Another problem is that he had to wind the weights back up sixteen times, and the water would have been stirred while winding. There is no evidence of a slip clutch in photographs of the device, which still exists. Winding up the weights would not have produced a known amount of heat, because the force and energy would vary with velocity. He said he used floats to prevent the water from rotating. Floats would not have been effective. The problem with rotating water is that the weights would drop at an increasing rate as the water rotation increased. The acceleration would reduce force on the cords, and it would add kinetic energy to the weights. The reason why Joule did those things and said those things is because real physicists were trying to do exactly what Joule was doing but failing. So Joule copied them but pretended to be successful. They gave up trying, while Joule ran to a complicit publisher with his lies. Concerning Joule's constant, there are theoretical problems on the relationships between force and energy which physicists do not understand. Some of the force would have been elastic creating stress instead of heat. Physicists have no theoretical concepts for the relationships between elastic and inelastic forces when stirring water. Joule's corrupt standards were demonstrated even more dramatically in experiments which he did with an electrical generator before switching to the wooden bucket experiment. He supposedly got the constant within about 10% doing a variety of those experiments. But they defied principles of physics besides being technically impossible. The basic procedure was to put a coil in a test-tube with water and spin it in a magnetic field for fifteen minutes. The kinetic energy on a hand crank was compared to the heat in the water. He used a galvanometer to measure electrical energy. It is a coil with a pointer, and the current flows through it. There were no concepts of volts or amps in those days. So he said he referenced the galvanometer to the blue color of a chemical in a solution. He then used its reading as a fudge factor which he called "unity." One of his errors was that a single instrument will not measure electrical energy. Both volts and amps need to be known. He had no theoretical concepts of what he was measuring. Sometimes he charged batteries. Some of the energy would go into the battery and some would heat the coil. He had no way of determining the energy going into the battery. In one experiment, he said he disconnected the wires and still got the constant. There should have been no force with the wires disconnected. Physicists say Joule must have known what he was doing, because he was only off by 3 ppt from the number they get. His number was 4.2 Joules per calorie; the modern number is 4.186 Joules per calorie. Instead of the modern measurement justifying Joule's experiments, it is Joule's experiments which tell the truth about the modern measurement. Since Joule did not have suitable theoretical concepts nor the slightest technical ability to produce such a measurement, the number has to be a contrivance. Physicists would say they do actual experiments. It only shows that they to are contrivers. Their methodology now days is not visible, but it seems to be referenced to electrical energy, which allows a very high degree of precision, except that electrical energy is even more difficult to relate to absolute values. When converting mechanical energy into electrical energy, a large amount of heat is lost. Due to this problem, the volt is apparently guessed at for absolute value, though it can be standardized with high precision. Regardless of how they conduct the modern experiments, Joule's constant is shown to be a contrivance due to the fact that the definition of energy is shown to be in error through my mathematics. Logic defines knowledge. Producing basic knowledge is the purpose of science. Physicists have been denying that science needs logic, because quantum mechanics and relativity are in conflict with logic. But physicists are wrong. There is no knowledge without logic and no purpose to science besides producing a logic consistent with the laws of nature, which have to have consistent relationships to be functional. Logic means consistent relationships.
By James P. Joule, Esq. Gentlemen, The apparatus exhibited before the association consisted of a brass paddle-wheel working horizontally in a can of water. Motion could be communicated to this paddle by means of weights, pulleys, &c., exactly in the manner described in a previous paper**. The paddle moved with great resistance in the can of water, so that the weights (each of four pounds) descended at the slow rate of about one foot per second. The height of the pulleys from the ground was twelve yards, and consequently, when the weights had descended through that distance, they had to be would up again in order to renew the motion of the paddle. After this operation had been repeated sixteen times, the increase of the temperature of the water was ascertained by means of a very sensible and accurate thermometer. A series of nine experiments was performed in the above manner, and nine experiments were made in order to eliminate the cooling or heating effects of the atmosphere. After reducing the result to the capacity for heat of a pound of water, it appeared that for each degree of heat evolved by the friction of the water a mechanical power equal to that which can raise a weight of 890 lb. to the height of one foot had to be expended. The equivalents I have already obtained are:—1st, 823 lb., derived from magneto-electrical experiments; 2nd, 795 lb., deduced from the cold produced by the rarefaction of air; and 3rd, 774 lb. from experiments (hitherto unpublished) on the motion of water through narrow tubes. This last class of experiments being similar to that with the paddle-wheel, we may take the mean 774 and 890, or 832 lb., as the equivalent derived from the friction of water. In such delicate experiments, where one hardly ever collects more than half a degree of heat, greater accordance of the results with one another than that above exhibited could hardly have been expected. I may therefore conclude that the existence of an equivalent relation between heat and the ordinary forms of mechanical power is proved; and assume 817 lb., the mean of the results of three distinct classes of experiments, as the equivalent, until more accurate experiments shall have been made. Any of your readers who are so fortunate as to reside amid the romantic scenery of Wales or Scotland could, I doubt not, confirm my experiments by trying the temperature of the water at the top and at the bottom of a cascade. If my views be correct, a fall of 817 feet will of course generate one degree of heat, and the temperature of the river of Niagara will be raised about one fifth of a degree by its fall of 160 feet. Admitting the correctness of the equivalent I have named, it is obvious that the vis viva of the particles of a pound of water at (say) 51° plus the vis viva which would be acquired by a weight of 817 lb. after falling through the perpendicular height of one foot. Assuming that the expansion of elastic fluids on the removal of pressure is owing to the centrifugal force of revolving atmospheres of electricity, we can easily estimate the absolute quantity of heat in matter. For in an elastic fluid the pressure will be proportional to the square of the velocity of the revolving atmospheres, and the vis viva of the atmospheres will also be proportional to the square of the velocity; consequently the pressure will be proportional to the vis viva. Now the ratio of the pressures of elastic fluids at the temperatures 32° and 33° is 480 : 481; consequently the zero of temperature must be 480° below the freezing-point of water. We see then what an enormous quantity of vis viva exists in matter. A single pound of water at 60° must possess 480° + 28° = 508° of heat; in other words, it must possess a vis viva equal to that acquired by a weight of 415036 lb. after falling through a perpendicular height of one foot. The velocity with which the atmospheres of electricity must revolve in order to present this enormous amount of vis viva must of course be prodigious, and equal probably to the velocity of light in planetary space, or to that of an electric discharge as determined by the experiments of Wheatstone. *The experiments were made at Oak Field, Whalley Range. **Phil. Mag. ser. 3. vol. xxiii. p. 436. The paddle-wheel used by Rennie in his experiments on the friction of water (Phil. Trans. 1831, plate xi. fig.1) was somewhat similar to mine. I employed, however, a greater number of "floats," and also a corresponding number of stationary floats, in order to prevent the rotatory motion of the water in the can. I remain, Gentlemen, Oak Field, near Manchester,
Potential Energy
Physicists also have a potential energy problem. Supposedly, energy is conserved as if a fixed quantity were being moved around. But in doing that, it often takes the form of "potential energy." Where is the energy in potential energy? Potential something is not the same as something. It's like spending more money than one has and calling the difference potential money. If energy is being converted to potential energy, then it is not being conserved. The logic is that it is possible to get the same amount of energy out of potential energy as was put into it, and therefore it is conserved some place in some form. Why then are not the gods of knowledge telling us what that place is and what that form is? The truth is that the place and form of potential energy is force. Force is one of the forms of energy. But physicists do not want to admit that force is a form of energy, because force can be amplified, and amplified energy would not be conserved energy. Physicists prefer pretense for convenience, so they don't have to expose their ignorance in trying to explain something which is not understood. If they can't explain amplified energy, then how can they know so much about space warps, worm holes and the rest of relativity? They are peddling the bliss of ignorance and calling it laws of nature. Consider a helicopter. It uses energy to stay motionless above the ground. It is said to have potential energy. If it drops out of the air, the potential energy is converted to kinetic energy. Guess what. It takes a fixed rate of energy to stay in the air for any amount of time, yet it always has the same amount of potential energy. It has the same potential energy after 10 hours as it had after 1 minute. Yet it uses 600 times as much energy in 10 hours as 1 minute. This occurs because gravity creates and destroys energy. Physicists deny that any such thing occurs. The proof that force is one of the forms of energy is in elastic collisions. When the two objects move toward each other, they have kinetic energy, and there us no force involved. As they collide, a force develops between them, as their motion decreases. Kinetic energy is converted to force. If force is interconvertible with motion, as Newton's laws indicated, then force is a form of energy.
What then is amplified force, as a lever produces it? It's unimaginable, because physicists do not know what force is. All they know about force is what it does. The corruption of physics began in 1686, when Gottfried Leibniz published the claim that force times distance is the basis of kinetic energy. Prior to that time the relationships between force and motion were on track and provided the basis for Newton's laws. At that time, there was a recognition of two types of force: dead force and living force. Living force is the force which Newton's laws are based on. It accelerates mass. Dead force is stress. It does not accelerate a mass. Living force is a repelling force, which pushes mass. Dead force is an attracting force, which pulls on mass and holds matter together. Living force is involved in transformations of energy, where energy is said to be conserved. Conserved means that the quantities of energy stay the same after an interaction as before. Dead force does not conserve energy. It includes gravity and stress, which can create and destroy energy. (So-called potential energy is energy which is created and destroyed by gravity.) And it includes levers, which amplify force. The result is that there are two alternatives for the definition of energy. There are contradictions between the two alternatives, and they cannot be resolved with existing knowledge. If energy is defined in terms of living force, transformations of energy conserve energy, but the dead force of levers amplify energy. If energy is defined in terms of dead force, levers conserve energy, but transformations based on living force do not, as shown with rockets in the mathematical proof. Should energy be defined in terms of dead force found in levers or living force found in transformations? Since conservation through transformation is considered to be the defining property of energy, transformations through living force should provide the basis for defining energy. In this case, my proof with rockets apply. But physicists based their definition of energy on the dead force of levers and contradict transformations based on living force such as heat produces in a rocket engine. There is no resolving the contradictions. Dead force and living force contradict each other. Picking one as the basis for defining energy is going to contradict the other. The proper alternative for defining energy is the living force which Newton's laws are based upon and which transformations of energy include, not the dead force which levers amplify. But physicists base their definition of energy on the dead force of levers. Physicists mindlessly assume the discrepancies can be accounted for in the exhaust of the rocket. There's no question where the energy is located. It's a question of defining energy in terms of transformation instead of nonsensical math. With ½mv², energy addition (including transformation) varies with reference frames, while addition of mv is independent of reference frames. The proof shows that, when defining energy as ½mv², the exhaust energy of two rockets can be the same, while the transformation is not the same. In tests 3 and 4 (Part 2), the rockets have the exact same burn times, while the ½mv² of one mass is 192, and the other is 770. One mass gets four times as much ½mv² as the other, while the rockets do exactly the same thing. If the rocket and exhaust can do exactly the same thing in both cases and add four times as much supposed energy to the forward mass of one than the other, then the energy is not coming from the fuel or rocket motor; it is simply a mathematical equation with no relationship to laws of nature. In other words, what I call proof is to show that the incorrect concept of energy has no relationship to fuel use. This should be considered proof in any rational mind. The correct analysis is that the equal and opposite forces created in the combustion chamber transfer equal and opposite amounts of kinetic energy to the exhaust and forward mass. This is consistent with kinetic energy being proportional to force times time and mv. What this proof shows is that the erroneous definition of energy separates energy addition from the transformation. Energy addition becomes a mathematical abstraction which changes with reference points and does not maintain a consistent relationship to the transformation which is supposed to be the source of the energy. The corrected definition of energy maintains a consistent relationship to the transformation, because the transformation produces a consistent and definable amount of force times time. The transformation does not produce a consistent amount of force times distance. The result of this mathematical proof is totally predictable, because force times time (Ft) does not equal ½mv² for an accelerating mass, and Ft is the only product of a rocket. The rocket produces a constant force, which means unchanging through time, while it has no relation to distance. In other words, if a rocket burns for one second, it will do the same thing at one thousand miles per hour as it will at one mile per hour. In fact, the speed is relative to reference frames. But the amount of ½mv² is different in each case. If a small rocket engine adds a one pound force for one second to a spacecraft moving at 25,000 miles per hour, a lot of energy is added; but if the same rocket engine adds a one pound force for one second to a roller-skate, a lot less energy is added according to the incorrect definition of energy. Same transformation; different energy. With the corrected definition of energy, the same amount of energy is added in both cases. While a constant powered rocket is accelerating, its speed goes from zero to several thousand miles per hour. All the time, the engine is doing the same thing independent of velocity. But the incorrect definition of energy says power is proportional to velocity. The explanation of physicists is that while a constant powered rocket is accelerating, the power shifts from exhaust to rocket. Supposedly, the power of the rocket mass increases with its velocity, while the power of he exhaust mass decreases, since its velocity is in the negative direction. Combining the forward mas and exhaust mass always balances their equations—that is relative to an external reference frame. Using an external reference frame is not valid for kinetic energy, because the forces act upon impact points. Where the force acts is where the energy gets transformed. Relative to an external reference frame, nothing happens while a rocket burns energy. Rockets show that energy is transformed in proportion to force times time (ft), which equals mass times velocity (mv) for an accelerating mass. Rockets usually burn fuel at a constant rate and produce a constant force. It means that a defined amount of fuel produces a consistent amount of force times time. Rockets do not produce a consistent amount of force times distance, which would equal mass times velocity squared. Rockets do not see distance. Distance relates to the starting point, and it varies with velocities, which vary with reference frames. In other words, a rocket will have a different velocity relative to the earth and to the moon. With different velocities, there will be different distances to the starting point. Physicists use a distracting irrelevancy to counter these facts. They show mathematics for the power of a rocket which is independent of reference frames. To do this, they relate power (rate of energy addition) to the separation velocity of the exhaust, which is always constant independent of reference frames. They then say equations balance, so there is nothing wrong with the definition of energy. But in the process they shift the reference from the rocket engine where the force acts (and creates separation velocity of exhaust) to an external reference for their equations which they claim balance. Balancing equations in that matter is a distraction, which does not directly test the definition of energy. But physicists indirectly prove the definition of energy wrong in doing so. When they use the separation velocity of the exhaust as the reference for rate of energy use, they throw out the distance to the starting point. If the starting point is not relevant to their argument, then energy is not transformed in proportion to force times distance. The false definition of energy is rationalized through shifting reference frames. Kinetic energy must be evaluated and defined in relation to the point where the force acts. Physicists do not. They define and evaluate kinetic energy relative to external reference frames. The problem with reference frames is inherent in the force times distance form of kinetic energy, because distance relates to the starting point, while the force does not act upon the starting point, and velocities are relative for starting points. Physicists make the inane argument that force times distance is work, not energy. But the so-called work and false kinetic energy are interchangeable, and whatever is most convenient will be used to represent energy. An example which they consider proof of kinetic energy being ½mv² is that it shows a net increase when energy is added to a system, while mv does not. The model for this point is an explosion blasting two objects in opposite directions. The question is whether there is a net increase in momentum. The quantity mv increases by the same amount in two opposite directions, because for every force there must be an equal and opposite force. The increase in one direction is given a minus sign; and when added to the mv in the other direction, the total is zero. The quantity ½mv², however, shows a net increase. Its velocity is squared, which converts any negative quantity to a positive quantity; and adding two positives always shows a net increase. That argument is a fallacy. It is not valid to put a minus sign by momentum when quantitating energy addition, because there is no such thing as a negative quantity of momentum. (In determining velocities, the negative sign has a different purpose.) An increase of momentum in two opposite directions is an increase in momentum. Therefore, momentum should be quantitated in absolute values when relating to energy. Here's another way of stating it. The original question is total quantity of energy. The minus sign changes the question to vectorial quality. After adding, it is then reinterpreted in terms of total quantity. Switching back and forth between total quantity and vectorial quality is not valid. Anything hit with the negative part of the mass will feel the same thing as if it were the positive mass. There is no such thing as negative energy, negative momentum or negative motion of mass. The assumption that energy must show a directional increase relative to an external reference frame is a fallacy. This point is demonstrated when heating a piece of metal. There is no directional increase in energy. Energy exists regardless of the direction of movement. Heat demonstrates this point. It is a randomization of motion. And it is called energy. To say that negative momentum cancels positive momentum is the same as saying half of the heat cancels the other half of the heat. For a correct analysis, energy addition must be evaluated relative to the point where the forces act or the impact point. Momentum increases in both directions relative to the impact point, when energy is added. In analyzing collisions, there is often no negative velocity, because the center of mass may be moving at a high velocity relative to an external reference frame resulting in both of the equal and opposite momentums having a positive velocity. Regardless of whether there is a negative velocity, no net momentum change occurs relative to an external reference frame, when energy is added, even though the momentums do change relative to the center of mass. The question is, must energy be able to change relative to an external reference frame; or is it something that only changes relative to impact points? Forces can only exist relative to impact points—not relative to an external reference frame, which is relative and infinitely variable. So the correct definition of kinetic energy should be the change in momentum relative to impact points or the points where the forces act. With rockets, the analysis of power by erroneous concepts is made relative to the point where the forces act by using the separation velocity of the exhaust as the reference. This strange twist allows the rocket equations to be balanced with the erroneous definitions. It also contradicts the premise that energy addition must occur relative to an external reference frame by the erroneous concepts. Rocket power is defined relative to the separation velocity of the exhaust (meaning impact point) but is then shifted to an external reference frame which results in indefinable power, as the second proof shows. Energy is defined by its transformation. Force transforms energy. And force acts on impact points. But force times distance is removed from impact points. When shifting reference frames, the arguments go in circles, but the math above proves that physicists are wrong. The math is quite rudimentary. Anyone who has studied a little calculus can verify it. ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ x' = rate of change for x = dx/dt (' is rate of change) mo = mass of rocket at start = 20kg plus payload (21 or 24 kg) m' = rate of mass loss = -0.01kg/s mt = mass of rocket at time T = mo + m't ve = separation velocity of exhaust = 103m/s (pos) F = force = -m've = -(-0.01)(103) = 10 newtons v't = acceleration at time T = F/mt ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ ◆ Force The rocket is arbitrarily given its basic characteristics. Then velocity is calculated from them. The analysis of a rocket's motion is based upon the fact that mass propelled from the exhaust produces a force in proportion to its acceleration; and an equal and opposite force acts upon the rocket. The force is based upon mass times acceleration (F=ma), which is the same as rate of mass loss (m'=0.01kg/s) times separation velocity of exhaust ( Acceleration v't = acceleration at time T = F/mt The acceleration of the rocket mass is force over mass (a=F/m). Since acceleration is velocity over time, it is denoted as v'. (The apostrophe is being used to denote division by time.) For any particular instant in time, acceleration is force over mass at that particular time. Mass Loss mt = mass of rocket at time T = mo + m't Since mass is being lost through the exhaust, the rocket mass varies with time. The mass at any particular time Velocity Velocity is derived from acceleration. Since acceleration is velocity over time, velocity is acceleration times time. In calculus, acceleration is the derivative of velocity with respect to time, which is the same thing as dividing something by time. The question is the opposite, knowing acceleration, what is the velocity. It is the anti-derivative of acceleration, which is the integration dt. Acceleration which changes with time (v't) is Velocity is the antiderivative of it, which is ∫v'dt. v = velocity = ∫v'dt = ∫10/(mo - 0.01t)dt For this mass (mo), we will use 20 kg to improve clarity. So we need to know this: ∫10/(20 - x)dx The antiderivative is: ∫10/(20 - x)dx = -10∫-dx/(20 - x) = -10ln(20 - x) + c The generic antiderivative for that type of equation is this: ∫du/u = ln(u) + c u = (20 - x) du = -dx "ln" is natural log base e. Before the actual equation is converted, it must be factored as follows: 10/(mo - 0.01t) = 103/(100mo - t) Its antiderivative (same as velocity) is -103ln(100mo - t) + c The quantity for c is calculated by using zero for time and changing the sign. The net result is this: v = velocity = ∫v'dt = ∫10/(mo - 0.01t)dt = ∫103/(100mo - t)dt = -103ln(100mo - t) + c (-c is quantity at T = 0) This formula is factored for time to get the desired quantity. Time is the only unknown, because the velocity is determined in the falling object analysis. Time v = -103ln(100mo - t) + c t = mo/0.01 - [(c-v)/103]ex ex is inverse of natural log for the preceding quantity. This equation for time is tailored in form and sequence for a calculator. The method of factoring velocity to get time is this: First, move a few things around to get this: (c-v)/103 = ln(100mo -t) Apply this principle: If a = lnb, then exa = b It says: If a is the natural log of b, then inverse of natural log of a equals b Now have a equal (c-v)/103 and b equal (100mo -t) Then inverse natural log of (c-v)/103 equals (100mo -t) ex[(c-v)/103] = 100mo -t Changing the signs and relocating is this: t = 100mo - ex[(c-v)/103] For sequencial entries on a calculator, it looks like this: t = mo/0.01 - [(c-v)/103]ex Fraction of Time for Payload The ratio of test mass to total mass is integrated with time. It is then averaged, and the average is multiplied times total time. The mathematical procedure for averaging nonlinear change is to integrate with the desired variable and then divide by the interval for that variable.
The mass ratio integrated with time is this: ∫ m/(mo - 0.01t) dt = -100mln(100mo - t) + c This quantity is divided by burn time to determine average mass fraction. It is then multiplied times burn time to determine the amount of time attributed to the test mass. Since dividing and then multiplying by the same number is unnecessary, the integration quantity is in itself the exact quantity desired. It represents the amount of time attributed to the test mass. Example for Exact Time For example, in the first test case, m = 4kg. The integration is this: -400ln(2400 - 10.6072) + c -c is quantity at t = 0 it is = 3,113.2896The integration quantity is 1.771779, which is exact time for test mass. Shortcut Formula for Burn-TimeThis can be applied to payload only: From Ft = mvt = mtvt/m've ----------------- 1. Energy: Historical Development of the Concept. R. Bruce Lindsay. 1975. p345. Dowden, Hutchison & Ross. 396pp. ISBN-10: 0470538813. ISBN-13: 978-0470538814 |
 In 1686, Gottfried Leibniz published a paper saying Descartes was wrong; it is not mass times velocity which is the conserved quantity of motion but mass times velocity squared (mv²). His basis was the claim that if a four kilogram object were dropped one meter, it would do the same thing as a one kilogram object dropped four meters. This result would conserve mass times velocity squared, but not mass times velocity. Through an analysis of relationships, Leibniz showed that force times distance is proportional to mass times velocity squared for colliding masses.
In 1686, Gottfried Leibniz published a paper saying Descartes was wrong; it is not mass times velocity which is the conserved quantity of motion but mass times velocity squared (mv²). His basis was the claim that if a four kilogram object were dropped one meter, it would do the same thing as a one kilogram object dropped four meters. This result would conserve mass times velocity squared, but not mass times velocity. Through an analysis of relationships, Leibniz showed that force times distance is proportional to mass times velocity squared for colliding masses.