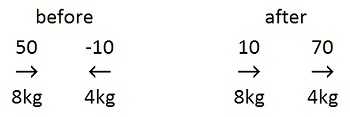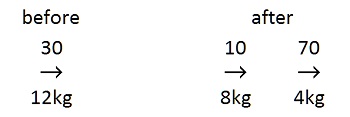5. Collision Analysis.

One of the common arguments given for kinetic energy being ½mv² is that it shows a net increase when energy is added to a system, while mv does not. The model for this point is an explosion blasting two objects in opposite directions. The question is whether there is a net increase in momentum.

The quantity mv increases by the same amount in two opposite directions, because for every force there must be an equal and opposite force. The increase in one direction is given a minus sign; and when added to the mv in the other direction, the total is zero.

The quantity ½mv², however, shows a net increase. Its velocity is squared, which converts any negative quantity to a positive quantity; and adding two positives always shows a net increase.

That argument is a fallacy. It is not valid to put a minus sign by momentum when quantitating energy addition, because there is no such thing as a negative quantity of momentum. (In determining velocities, the negative sign has a different purpose.) An increase of momentum in two opposite directions is an increase in momentum. Therefore, momentum should be quantitated in absolute values when relating to energy.

Here's another way of stating it. The original question is total quantity of energy. The minus sign changes the question to vectorial quality. After adding, it is then reinterpreted in terms of total quantity. Switching back and forth between total quantity and vectorial quality is not valid. (Here's a page on the negative momentum issue.)

The assumption that energy must show a directional increase relative to an external reference frame is a fallacy. This point is demonstrated when heating a piece of metal. There is no directional increase in energy.

Energy exists regardless of the direction of movement. Heat demonstrates this point. It is a randomization of motion. And it is called energy. To say that negative momentum cancels positive momentum is the same as saying half of the heat cancels the other half of the heat.

For a correct analysis, energy addition must be evaluated relative to the point where the forces act or the impact point. Momentum increases in both directions relative to the impact point, when energy is added.

In analyzing collisions, there is often no negative velocity, because the center of mass may be moving at a high velocity relative to an external reference frame resulting in both of the equal and opposite momentums having a positive velocity. Regardless of whether there is a negative velocity, no net momentum change occurs relative to an external reference frame, when energy is added, even though the momentums do change relative to the center of mass.

There is a contradiction in saying that the net energy increases, while the net momentum does not. Momentum is the motion of a mass. If the motion of the mass has no net increase, how could there be a net change in the kinetic energy, which is said to be the energy of motion?

As a matter of fact, kinetic energy as ½mv² is not in the motion of the mass, because no mass can move at velocity squared. Its motion is first said to be its velocity (Momentum and velocity are both motion.); and its velocity is not its velocity squared. So ½mv² is an abstraction apart from the motion of the mass. The question is, can energy really be an abstraction, if it is used in discrete quantities as fuel? Fuel is more than an abstraction; so the energy defined by the equation must be more than an abstraction. Momentum is perceivable as mass and velocity; but ½mv² is not.

Simple Collisions.

To demonstrate the principles of collision analysis, a simple type of collision will be analyzed, which is a head-on elastic collision of two masses. The predictability of the collision is dependent upon the fact that the center of mass (CM) maintains the same velocity after the collision as before. Also, the momentum relative to the center of mass stays the same for each mass but reverses directions.

shows object velocities

Mass 1 is 8kg moving right at 50m/s. Mass 2 is 4kg moving left at 10m/s. The net momentum is the sum of the two momentums, when the velocity left is given a negative sign.

NM = m₁v₁ + m₂v₂ = 8(50) + 4(-10) = 360

The velocity of the center of mass (vCM) equals the total momentum divided by the total mass.

vCM = 360/12 = 30

The initial velocity of each mass relative to CM is its original velocity minus vCM.

m₁: 50 - 30 = 20 m₂: -10 -30 = -40

Changing the sign produces the same velocity relative to CM after the collision. The velocity is then converted to the original reference frame by adding the velocity of CM.

m₁: -20 + 30 = 10 m₂: 40 + 30 = 70

A simpler procedure is possible by analyzing the velocities only. The final velocity of each mass will be twice the velocity of CM minus its velocity before the collision.

2vCM - v(before) = v(after)

m₁: 2(30) - 50 = 10 m₂: 2(30) - (-10) = 70

With these numbers, the mv and ½mv² are calculated.

m₁ m₂ total

mv ½mv² mv ½mv² mv ½mv²

before: 400 10,000 -40 200 360 10,200

after: 80 400 280 9,800 360 10,200

This example only shows that mv and ½mv² are both conserved during elastic collisions (the total columns). The bigger question is what happens when energy is added to the system.

Adding Energy.

To demonstrate the addition of energy, the following example will start with the 8kg and 4kg masses combined and moving right at 30m/s; and then an explosion will separate them with a force averaging 1600N (newtons) for 0.1 seconds. First acceleration will be determined as a = F/m; and then velocity will be determined as v = at. (Force left is minus.)

m₁: a = -1600/8 = -200 m₂: a = 1600/4 = 400

m₁: v = -200(0.1) = -20 m₂: v = 400(0.1) = 40

These velocities are relative to CM; so they must be added to vCM to get velocities relative to an external reference frame.

m₁: -20 + 30 = 10 m₂: 40 + 30 = 70

So the result is this:

shows object velocities

The resulting levels of mv and ½mv² are:

	m₁		m₂		total
	mv	½mv²	mv	½mv²	mv	½mv²
before:	240	3,600	120	1,800	360	5,400
after:	80	400	280	9,800	360	10,200

The table shows that relative to an external reference frame the energy added by the explosion increased the amount of ½mv² but not the mv. (360mv before and after). The usual assumption is that this demonstrates that adding energy to a system does not change momentum. However, relative to the impact point, the momentum went from 0 to 160 in each direction.

The Corrected Concept.

So the question is, must enegy be able to change relative to an external reference frame; or is it something that only changes relative to impact points? Forces can only exist relative to impact points—not relative to an external reference frame, which is relative and infinitely variable. So the correct definition of kinetic energy should be the change in momentum relative to impact points or the points where the forces act.*

The collision analysis is not a major proof in itself; but the perspective on collisions Would be improved with the correct definition of energy. The same is true of most points being made here. The mathematical proof is in applying rockets to the falling object issue, which is shown in the rocket section.

*Notice in the rocket section that the analysis of power by erroneous concepts is made relative to the point where the forces act by using the separation velocity of the exhaust as the reference. This strange twist allows the rocket equations to be balanced with the erroneous definitions. It also contradicts the premise that energy addition must occur relative to an external reference frame by the erroneous concepts.

Rocket power is defined relative to the separation velocity of the exhaust (meaning impact point) but is then mixed with an external reference frame which results in indefinable power, as the second proof shows.

Energy is defined by its transformation. Force transforms energy. And force acts on impact points. But force times distance is removed from impact points.

Physicists need to apply their equations to all reference frames. Distance is not universal enough to apply to all changes in reference frames. This statement might seem too trite to believe, but the proofs here show that it is true.