It should be apparent that when engines use fuel at a constant rate they produce a constant force. The rate of fuel use is approximately the rate of energy transformation. Some of the transformed energy goes to heat; but what the useable product is supposed to be depends upon definitions. It would seem that the only useable product of an engine is force. But when energy is considered to be ½mv², force does not entirely correlate with the rate of energy addition. The rate of energy addition is then proportional to force times velocity. Since velocity increases during acceleration, the rate of energy addition increases, while force stays constant.
Power corrupted by Velocity.
The relationship between power
and FV is demonstrated by factoring equations.
½mv²/t = ½m(v/t)v = ½mav
= ½Fv
The ½ is simply dropped (or removed by calculus), because power relates to the instantaneous velocity, while the ½ had the purpose of averaging the
velocities to relate directly to distance in Fs.
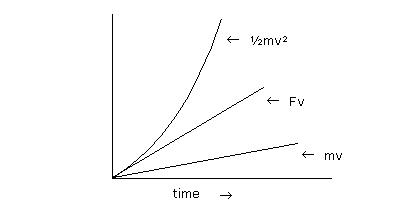
When a constant force is accelerating a mass, the ½mv² increases exponentially, and Fv and mv increase linearly. To demonstrate the dynamics, consider a 5kg mass which is accelerated at 10m/s/s.
The force is constant: F = ma = 5(10) = 50
The ½mv² increases exponentially, as shown in the table. When graphed, it shows an upward curve. Its rate of change, Fv, is constantly increasing showing a straight line upward on the graph.
| sec. |
v =
at |
Ft =
mv |
Fs =
½mv² |
Fv |
| 1 |
10 |
50 |
250 |
500 |
| 2 |
20 |
100 |
1,000 |
1,000 |
| 3 |
30 |
150 |
2,250 |
1,500 |
| 4 |
40 |
200 |
4,000 |
2,000 |
|
The Nonlinear Power of Engines.
If the mass is accelerated by an engine, it seems that fuel would be used at a constant rate, because the force is constant. The rate of fuel use should correlate with energy increase. But the rate of energy increase as Fv is not constant; it is increasing. If however, the energy is in proportion to mv rather than ½mv², it shows a constant rate of increase. The rate of increase in mv is in proportion to force only, as factoring demonstrates.
mv/t = ma = F
Since the force is constant, it parallels the rate of fuel use, which would presumably be constant.
Physicists, however, deny that a constant rate of fuel use by an engine produces a constant force while accelerating a mass in the absence of friction. The force would be decreasing under such conditions, according to the equations based upon ½mv² being energy.
Such a conclusion appears illogical. A constant rate of fuel combustion should produce the same number of energized particles per second, each with the same energy, regardless of the motion of the total mass. Doubling the velocity of the total mass should not cause the particles to produce half as much force.
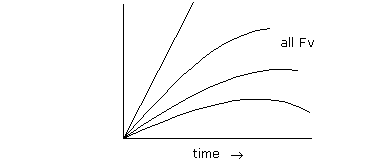
The graph below shows various decreasing rates of acceleration, as would occur if force decreased with velocity. It is impossible to get a constant power as Fv. The power must start at zero and increase with a decreasing curve, while fuel use is constant. There is no straight, horizontal line, which means reducing acceleration does not produce a constant power.