|
| Gary Novak Background
|
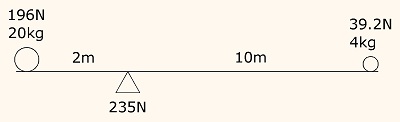
8. Levers and Fields Mysteriously, levers arrange stress forces in such a way as to amplify force. Since force is the ability to create motion, levers can apparently amplify momentum. However, when the total energy of a lever is analyzed, linear momentum is conserved through a lever, but angular momentum is not. Whatever this means, there is nothing in the laws of nature which says energy must be conserved to any greater extent than momentum is conserved. Analyzing Momentum through a Lever To analyze momentum through a lever, we will first consider a balanced lever, as shown below. F = mg = m(9.81) The fulcrum is rigid and has 235N of force on it producing a counterforce to the total force on the ends of the lever. If the lever were set in motion, it would stay balanced; but there would be an invisible shift in stress forces as it became vertical. If the 4kg mass acquired a velocity of 5m/s, the 20kg mass would have a velocity of 1m/s, because it only moves 1/5 as far in the same amount of time. The momentum would be the same for each mass: 4(5) and 20(1). If the masses were accelerated by adding 120N of force to the 4kg mass, what would happen? (The force which is accelerating the first mass is not pushing on the lever.) Apparently, 20N of force would be transferred to the opposite side. Then 100N of force would accelerate the small mass at: a = F/m = 100/4 = 25m/s/s. The 20N transferred to the other side would be amplified to 100N acting upon the large mass; and its acceleration would be: a = 100/20 = 5m/s/s. The acceleration ratio would be 5/1 as required by the distance ratio. If the acceleration occurred for 0.1 seconds, the velocities would be 2.5m/s and 0.5m/s. The momentum of the small mass would be: 4(2.5) = 10; and for the large mass: 20(0.5) = 10. The momentum of each mass would be the same but in opposite directions. The complete input force, called impulse, would have been the equivalent of 12 momentum units, being proportional to force times time: 120(0.1) = 12. The net momentum on the fulcrum is also 12 units, since it saw 20N of force from one side of the lever, and 100N from the other (for 0.1 sec.). So the input and output momentums each appear to be 12 units. But since the circular momentum increased by 20 units (10 on each side), there must have been an energy absorption, such as an inelastic collision would create. The increase in circular momentum looks like the creation of energy, but if it were removed, the same amount would come out as went in, which is 12 momentum units. The total momentum added went to the fulcrum, which means no energy was amplified. When automobile gears are considered, it appears that energy is following a force-distance rule. But the force on the fulcrum in the gearbox is not considered. That force is pushing on the auto and works against some other force. The distance with that force is negligible, which makes it irrelevant with the force-distance analysis. But in reality, creating a force takes energy regardless of the distance element. What this means is that the usual analysis ignores the energy acting upon the fulcrum. It cannot be ignored. It works against something, such as gravity, the earth or the combustion chamber. When considering this part of the energy, the force-distance analysis does not conserve energy, but the force-time analysis does. In other words, levers or gearboxes only amplify circular momentum, not linear momentum. This increase in circular momentum cannot be captured or used as amplified, linear momentum. Therefore, it is not relevant to applications. There is no reduction in linear momentum resulting from the mysterious increase in angular momentum. What energy as fuel does in levers or gears is too mysterious and complex to determine, but the rocket analysis shows that fuel is transformed as momentum, not ½mv². A Collision to add Energy So let's analyze a collision which adds the energy. If a 2kg mass impacts the 4kg mass, it would apparently see the equivalent of 0.8kg of additional mass, because 20N were transferred across the lever, while the acceleration was 25m/s/s for the 4kg mass: m = F/a = 20/25 = 0.8kg. Since the 4.8kg apparent mass acquired a velocity of 2.5m/s, the velocity of the center of mass (vCM) must have been half that, or 1.25m/s. [v(after) = 2vCM -0]. The momentum relative to the center of mass (in both directions) would be 1.25(4.8) = 6. So the velocity of the 2kg mass would be 3m/s relative to the center of mass, or 4.25 relative to an external reference frame. After the impact, the velocity of the 2kg mass would be -1.75m/s. v(after) = 2vCM - v(before) = 2(1.25) - 4.25 = -1.75 So the 2kg mass which provided the energy had an original momentum of 8.5 units, and a final momentum of -3.5 units, for a total exchange of 12 units. Of the 12 units exchanged, 10 went to the 4kg mass; and 2 went through the lever causing it to be amplified to another 10 units for the 20kg mass. The amplification of momentum results from 12 momentum units being directly exchanged, while 20 momentum units were acquired by the two masses on the lever. But again, the force on the fulcrum conserves the linear energy as momentum. The ½mv² appears to be conserved as angular motion, but it creates a force on the fulcrum which is ignored as being a miniscule amount of energy. The force on the fulcrum usually acts upon the earth or its gravity. If energy is proportional to force times time, the force acting upon the earth and its gravity is significant energy. But when energy is considered to be proportional to force times distance, the force acting upon the earth and its gravity is considered to be trivial to a point of irrelevance. This force is not irrelevant, because significant energy is required to create such a force. Circular energy is amplified by levers, because stress creates and destroys energy. It is a source of energy, but only for very short distances. Stress cannot be used as a continuous source of energy. When the circular energy is re-linearized, it is de-amplified. It is only the two directionality of a fulcrum that produces this effect, not all circular motion. Circular, amplified energy cannot be used, because it de-amplifies when it is linearized. Therefore, it is questionable whether it should even be viewed as amplified energy. It is not all amplified in the same direction. How much energy it should represent is an arbitrary mathematical analysis. The motion is in all directions, and any force on it adds force to the fulcrum. The real energy is what can be extracted, and it is not amplified. Applications all involve linearized energy, which is not amplified. Therefore, it is inappropriate to define or quantitate energy on the basis of circular, amplied energy. Gravity Another example of energy not being conserved is gravity. Gravity creates and destroys energy by creating a force when a mass enters a field. Physicists say that when an object is lifted against gravity, it acquires a potential energy in proportion to the force times the height. Since the force is the same at both levels, the potential energy must be in the height only. But distance without force cannot change the motion of a mass. The potential energy is not in the distance but in the gravity. Potential energy could be more correctly described as a force which is not accelerating a mass—meaning a stress force. In this case, gravity creates the opposing force; but sometimes, another stress force does. Similarly, physicists indicate that no energy would be required to hold an object off the ground at a fixed height, because the distance does not change. How long would they want to hold a heavy object off the ground? It takes energy to do so. The energy is proportional to force times time. If the object is not held in place by a stress force, then the counterforce must be the equivalent of a force which accelerates a mass. Apparently, the reason why a lever can amplify force is because compression creates force, just as gravity does. Compression and gravity produce continually recreated forces; and unless countered by a stress, they must be countered by a source of energy. Fields A field appears to be a medium with waves in it. Physicists, however, do not consider fields to have mediums. Physicists supposedly determined that electromagnetic waves are not conducted through a medium, because an experiment of a century ago (since repeated) failed to find a difference between the velocity of light parallel to the motion of the earth and light perpendicular to it. But a negative result in science without a positive result usually means that the experimental design was inadequate. The conclusion of the physicists was that the constant velocity of light is not determined by a medium; and since it would not be constant if it were determined by the emitting point, it must be determined by the receiving point. One of the contradictions is that different receiving points can have different velocities; and therefore, electromagnetic waves would have to have an infinite number of velocities simultaneously. Obviously, electromagnetic waves must be a result of a variation in a medium, though in some cases, there are particles moving with the waves. The velocity is then determined relative to the medium. Since the energy equation is incorrect, relativity must be incorrect, because it depends upon the energy equation. Relativity indicates that as velocity increases, mass, time and distance change. It is not valid to alter such basic properties, because they must be used as yardsticks to measure with. Volts and Watts With corrected definitions, voltage is a field, not a force. Watts correlate with units of force. Just as a mass must enter a field of gravity to create a force, electrons must enter a field of voltage to create a force. The number of electrons per second times the voltage determines the watts of force, which is the rate of energy addition. Electrons per second would be similar to mass per unit time in a field of gravity, because masses would be transient, and forces would be changing, in a large scale system of gravity. Force is Energy Force and motion are interchangeable forms of energy. For example, with elastic collisions, motion first exists without force. Then force replaces motion, until all motion stops. At that point, all of the energy is in the force. So force is not just the rate of energy addition; it is also a form of energy. But since force is transitory, while motion is not, force must be multiplied times time to produce a quantity of motion. Therefore, creating or amplifying force is creating or amplifying energy. The conservation of energy is not an absolute phenomenon. Gravity creates force and energy. Levers amplify force and energy. To conserve an abstraction, when energy is supposed to be created or amplified, demonstrates that the abstraction is not energy. In other words, the analysis of ½mv² removes much of the complexity of nature, besides contradicting the logic. Its lack of a relationship to actual events results in the basic questions being erased rather than answered. The basics of energy are nearly unstudied because of the obstacles created by the analysis of ½mv². Elastic Force A related question is how elastic and inelastic forces mix together. When stirring water, as Joule supposedly did, there is an unknown ratio of elastic to inelastic forces. The assumption of the measurement of Joule's constant by stirring water is that all of the force is inelastic and creates heat. But that is not true. A rowboat shows the difference. If the oars are pulled slowly, little elastic force is produced. If the oars are pulled hard, more elastic force is produced. The ratio of elastic to inelastic force varies each time. Physicists don't know that elastic force occurs when stirring liquids. If it didn't, there would be no motion forward for a boat being rowed. Only the elastic force moves the boat forward, while the inelastic force heats the water. Inelastic force randomizes motion as heat, while elastic force maintains linearized motion. |