Gary Novak Energy Home   Background Tutorial 1. quick proof 2. rockets 3. history 4. definitions 5. collisions 6. falling objects 7. engines 8. levers   Second Proof Concise Math Math Explained Joule's Constant Potential Energy Living Force Counter-Argument Word Summary Printable Summary Joule's Publication

▼▼▼     1. Quick Summary of Proof 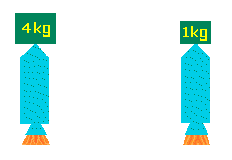  The proof shows that the fuel used by a rocket does not correlate with the addition of ½mv² but the addition of mv of an attached mass. To show this, a rocket is applied to the falling object issue. The math is shown on the falling object page and rocket page. Part One: Neither force x distance nor ½mv² is kinentic energy. A 4kg object dropped 1m (meter) has the same amount of ½mv² as a 1kg object dropped 4m, because force times distance equals ½mv² for an accelerating mass. But a rocket accelerating the masses to those velocities requires twice as much energy as fuel for the large mass as for the small one.* Therefore, both masses do not have the same energy; the rocket does not transform energy in proportion to ½mv²; ½mv² is not kinetic energy; and a gallon of fuel does not produce a consistent amount of ½mv². Part Two: mv (momentum) is kinetic energy. A 4kg object dropped for 1s (second) has the same amount of mv (momentum) as a 1kg object dropped for 4s, because force times time equals mv for an accelerating mass. A rocket accelerating the masses to those velocities uses the same amount of energy as fuel for both masses. Therefore, both masses have the same amount of energy; the rocket transforms energy in proportion to mv; mv is kinetic energy; and a gallon of fuel produces a consistent amount of mv. In other words, the rate of energy use (power) by a rocket engine is proportional to the increase in momentum of the foward mass, not the ½mv² of the forward mass. *Note. The calculated energy applies only to the mass in question, not the rocket mass; and there is zero error in the calculation.   Mathematics  (rocket page) Energy Home Top