|
The Cause of Ice Ages and Present Climate |
Fudge Factor for so-called Settled Science
Therefore, upon doubling the amount of carbon dioxide in the atmosphere, the fudge factor says the primary temperature increase is 1°C. Then secondary effects (mostly due to water vapor) increase the result to 3°C. The fudge factor was determined by Myhre et al, 1998—pdf using radiative transfer equations. It says, the amount of heat added to the atmosphere (watts per square meter) equals 5.35 times the natural log of the amount of CO2 after an increase divided by the amount before. This equations states that doubling the amount of CO2 in the atmosphere (natural log of 2 times 5.35) will result in a heat increase of 3.708 watts per square meter. It's total nonsense, as there are no square meters in the atmosphere. But the result points to a change in energy going into and out of the atmosphere when looking at the cross-sectional area of the earth from a distance, where the sun's energy is 1367 W/m². This fudge factor was derived from fake radiative transfer equations. It supposedly shows the primary effect of global warming. In other words, the supposed result of the radiative transfer equations was converted into a rudimentary fudge factor for simple calculation of the result. It says that doubling the amount of carbon dioxide in the air, even from one molecule to two molecules, would add 3.7 watts per square meter of energy to the earth. A three component equation supposedly takes care of the complex effects of carbon dioxide heating the atmosphere. The problem is not that the fudge factor is a simplified representation; the problem is that there is no science to the calculation. C over C sub zero is the increase in CO2. The question is what would happen upon doubling the amount of carbon dioxide in the air. For this the ratio of C over C sub zero is 2. So the fudge factor is 5.35 times the natural log of 2, which is 3.7 watts per square meter. Climatologists call this effect "forcing." This subject is discussed in the 2001 publication of the IPCC, chapter 6 (6.3.1) http://www.ipcc.ch/ Stefan Rahmstorf (in a book by Ernesto Zedillo, 2008) cited the IPCC saying: "Without any feedbacks, a doubling of CO2 (which amounts to a forcing of 3.7 W/m2) would result in 1°C global warming, which is easy to calculate and is undisputed." The fudge factor is totally invalid, because it removes saturation. Nothing can remove saturation. Nowhere is there an explanation of how or why saturation was removed in the calculation of the fudge factor. The fudge factor is derived out of muddle which shows no other purpose than removing saturation from the effects. The most recent, and assumed to be definitive, derivation for the fudge factor was the use of radiative transfer equations by Myhre et al, in 1998. There was no logic in using the radiative transfer equations besides muddling the subject to remove saturation, because there was no known mechanism, and the process of calculating radiative transfer tells nothing of relevance to any suggested mechanism. Supposedly, the mechanism is a reduction in radiation emission by 3.7 W/m² at the top of the atmosphere. Not quite. The same amount of radiation is emitted as enters from the sun, which is 235 W/m². So the explanation is that this 235 W/m² (or relevant proportion) must leave at a higher temperature. There is no theoretical method of calculating the fudge factor, because radiation absorption by CO2 must be measured, it cannot be calculated. So why do a calculation after measuring the result? The measured results shows saturation in 10 meters, while the calculation shows almost no saturation throughout the atmosphere. Muddling the subject and contriving the endpoint is the only reason for doing a calculation. The fudge factor is extremely absurd. It shows the same result no matter how little CO2 is in the air. If there is one molecule of CO2 in the air, doubling it to two molecules will supposedly add the same 3.7 W/m² to the entire surface of the earth.
A fudge factor (or constant) removes all variation and natural influences. Supposedly, all complexities were modeled into the fudge factor with total precision, but such things as clouds, humidity, temperature variations and absorption by oceans are too complex and variable to be calculated or predicted. Yet the calculation supposedly had only about 1% error.
There is no identifiable starting point for most radiation. It is emitted and absorbed from every molecule in the atmosphere and on the surface of the earth. So there is no identifiable starting point for the radiative transfer equations used to determine the primary effect (fudge factor). Analysts add a few angles to their radiative transfer equations to show their wizardry with geometry, but they can't scratch the surface of the undefinable complexities, because radiation is emitted and absorbed in all directions from every molecule with 15-30% going directly into space from all positions in the atmosphere. How the radiation equilibrates with energy entering from the sun is beyond analysis. With 15-30% of black body radiation going around all greenhouse gases, only 4 cycles of emission and re-absorption would send all absorbed energy into space. In other words, the energy does not have to be emitted and absorbed a thousand times to get from the surface of the Earth to outer space. The fudge factor is the primary effect supposedly produced by CO2, determined through calculations, and then modeling is used to determine fake secondary effects. A primary effect cannot be distinguished from secondary effects in the atmosphere. Such an effect would have to be theorized. The primary effect represented by the fudge factor deals with radiation, which gets absorbed by the oceans in major ways which cannot be evaluated. There is no concept of how much radiation is going where. The secondary effect deals with temperature, where oceans can add heat to the atmosphere, but the atmosphere cannot add heat to the oceans, because there is way too little heat capacity in the atmosphere compared to the oceans. The fudge factor is a substitute for a mechanism. Since no mechanism could be found or synthesized, a result was contrived as if it came from a mechanism. It supposedly shows how much heat carbon dioxide produces in the atmosphere. The pretense is that the effect of global warming by carbon dioxide can be represented by a simple equation. Complexities in science can never be represented by simple equations. The fudge factor has no relationship to objective reality. It's like the endless constants in physics, such as Planck's constant or the Stefan-Boltzmann constant, which are totally contrived and have no valid basis, because the complexities do not reduce to simple equations. They are nothing but a product of fakery which has replaced real physics.
Distance is the Critical Factor The primary question is how much radiation is absorbed by carbon dioxide upon increasing concentrations. The number of molecules can be represented with distance, since there will be so many molecules per unit of height in the atmosphere. For example, Heinz Hug did a measurement in a tube in a laboratory to show absorption. If the amount of carbon dioxide in the air is doubled (2x), the distances reduce to one half. This logic easily proves the whole concept of greenhouse effect to be a sham, because changing the distance is not changing the heat. In fact, the critical molecules on the shoulders of the peaks are spread so thin in the atmosphere that they cannot produce significant temperature increase. (The shoulder molecules are in slightly different energy states due to stretching of bonds, as if they were different molecules. The 5% shoulders have twenty times as much space between each, because there are one twentieth as many of them.)
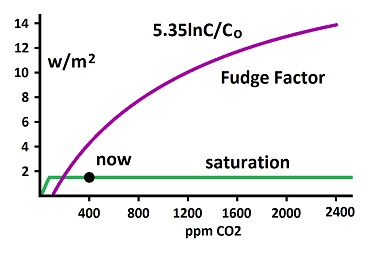
Due to saturation, the curve for heat absorption by CO2 cannot keep increasing. Instead it would rapidly level off, as shown by the green line in this graph: The reason why the curve does not start at zero is because it is too self-contradictory. It does not get to the claimed, present state, unless the curve is slid over. Notice that any scale can be used at the bottom without the heat scale on the left side changing. This means doubling CO2, even from one molecule to two molecules, will add 3.7 watts per square meter to the surface of the earth. Some climatologists will state an upper range for the fudge factor, such as 1000 ppm, and some will include a lower range, such as 250 ppm. Adding such restrictions is an arbitrary attempt to hide the ridiculousness of the fudge factor. There is no reality to the fudge factor, because it erased saturation, which cannot be erased. To add restrictions to a total contrivance is nothing but more contrivance. The fudge factor curve is self-contradictory regardless of any range, because it produces the same 3.7 W/m² for doubling any concentration within any stated range. If 250 ppm is doubled to 500 ppm, 3.7 W/m² supposedly occurs. If 500 ppm is doubled to 1000 ppm, the same 3.7 W/m² supposedly occurs. This is the same absurdity as doubling one molecule to two molecules and getting 3.7 W/m²—only being more obscure in a narrower range. There is nothing in nature that would change the relationships at lower concentrations. Rationalizers say the nonlinearity (logarithmic curve) is a good representation, because it shows that saturation becomes more of an influence with increased concentrations. In saying that, they admit that saturation is influencing the result, yet they reduce the effect to a bend in the curve. In actuality, saturation totally prevents any increase in temperature from occurring. The significance is shown in the above image, where saturation totally stopped any effect long ago, while the fudge factor shows only minor reductions. The fudge factor uses a natural log curve, which is a contrivance, as it eliminates complexities. A math function cannot represent the complexities which have unique factors to them, as science always does. A natural log curve creates a hypothetical which cannot represent the large number of interacting complexities. A curve must consist of measured points in such complexities, not a hypothetical math function. This point tends to be true of all complexities of science—that math and curves must be produced through measurements rather than math functions. Engineering can use math functions as simplified representations because of the absence of complexities and the ability to separate out effects which are unvarying. Physicists try to apply the engineering process to their version of science, and they omit too much complexity doing that. Saturation was Reduced to a Trivial Amount With the fudge factor, a small amount of saturation creates the bend in the curve. But the saturation is actually about 10,000 times greater than the fudge factor curve indicates. Measurements, such as that of Heinz Hug, show that the center of the main absorption peak saturates in 10 meters. To get saturation to occur at a height of 10 km would require one thousandth as much saturation. But 10 km is still in the normal atmosphere (troposphere). To get non-saturation of any significance, as indicated by the fudge factor, at least ten times as much distance is required, or one tenth as much saturation, which would be 10,000 times as much as indicated by the fudge factor. To determine the effects of saturation, the question is how far should radiation travel before being totally absorbed. Nowhere in prevailing climatology is there any indication of distance being considered. Implicitly, the radiative transfer equations calculated a series of parcels from the bottom to the top of the troposphere. There is no logic for doing that, since an unfathomable mechanism is usually said to occur at 9 km up, and it is independent of the distance to the earth's surface. But radiation traveling from the surface to the fake mechanism requires at least 9 km to get there. So the distances implied by the radiative transfer equations need to be quite large. The effect of radiative transfer equations is to show that less radiation leaves the atmosphere than enters from the sun, until equilibrium is restored at a warmer temperature for the atmosphere. In doing so, saturation is reduced to trivia, and the mechanism is reduced to simple absorption of radiation throughout the atmosphere, based on the premise that the radiation all starts at ground level and moves upward. Most energy gets into the atmosphere through conduction, convection and evaporation. Another problem is that the planet is cooled by radiation which goes around greenhouse gases to establish equilibrium, which cannot be determined through mathematics. A gate half open will not keep in half the sheep. The assumption is that equilibrium is created at the top of the atmosphere, but, as the image on the right shows, radiation escape and equilibrium are created throughout the atmosphere. Direct Measurements Cannot be Replaced by Calculations Direct measurement shows saturation to occur in 10 meters for CO2 at ground level. No atmospheric complexities need to be considered over such a short distance. Therefore, there is a high degree of reliability in the measurement. But global warming claims are based on calculations which are designed to show almost no saturation throughout the normal atmosphere (troposphere). Infinite complexities in the atmosphere must be considered when the distance covers the whole atmosphere. Those complexities are too random and undefinable for real calculations. For example, overlapping and interacting radiation waves are too numerous and complex to be evaluated, and the amount of radiation being absorbed and emitted by the oceans cannot be determined, not the least reason being that the oceans are so heterogeneous with mountains and rivers of temperature variation that surface temperatures cannot be predicted. El Ninos are unpredictable due to the infinite unknowns. What it means is that a calculated method of determining radiation absorption (actually transmission) through the atmosphere is so impossible that it is totally contrived; and it is unnecessary, because the measurement is extremely reliable in showing total absorption in 10 meters. The calculation is being used for nothing but muddling the subject and contriving the result. Afterwards, converting radiation into temperature is impossible for the same reasons. In addition to the complexities, the temperature will depend upon the amount of time between radiation absorption and re-emission, which is too complex and unknown.
These points are made by Norm Kalmanovitch in a discussion on Judith Curry's web site here: http://judithcurry.com/2011/ Kalmanovitch points out that the calculations (in the radiative transfer equations and originating with Hansen et al going back to 1981 [5]) deal with radiation intensity which cannot be converted to temperature due to infinite complexity. He also points out that the curve cannot be chopped off for low values, which show the absurdity. Removing the evidence of absurdity is not a scientific analysis but an obfuscation. Kalmanovitch's points are brushed off with contempt and ridicule by other commenters who claim the majority scientists cannot be wrong in relating to the fudge factor as an unquestionable law of physics. This mockery and contempt for real science criticism is the entire problem with the global warming issue.
A described procedure for quantitating the primary effect is to calculate the amount of radiation obstructed at the top of the atmosphere and then using the Stefan-Boltzmann constant to convert radiation into temperature. There are three major problems with this: One, the radiation cannot be calculated; two, the Stefan-Boltzmann constant is off by a factor of about twenty; and three, what happens at the top of the atmosphere has no relationship to what happens at the bottom, where humans are concerned with near surface temperatures. The amount of radiation obstructed at the top of the atmosphere cannot be calculated. Satellites can crudely measure it, but why do a calculation when it can only be measured? The calculation is nothing but a muddling process for concealing the absurdity of the method. The reason why such radiation cannot be calculated is because it comes out of a well that is way to random and complex. It is the well of heat and radiation interacting throughout the atmosphere, while radiation exits in complex and variable ways while establishing equilibrium with the amount of radiation entering from the sun. The Stefan-Boltzmann constant says how much radiation is emitted from matter at any temperature. It is not a real representation of anything that actually happens in nature, because emitted radiation depends upon chemistry, which is highly variable. The variations are adjusted for as "emissivity" or its inverse, "absorptivity." But worse, the Stefan-Boltzmann constant shows about 20 times too much radiation at normal temperatures. If it is reduced by a factor of 20, the excess absorption of radiation claimed to result from CO2 changes from 3.7 W/m² to 0.19 W/m², which is one twentieth as much radiation. If the radiation is held at 3.7 W/m², the temperature change of the primary effect goes from 1°C to 17.8°C. It shows the problem of starting at the desired end point and going backwards to rationalize it. When the input quantities are corrected, the end result gets ridiculous. Calculations (as here): Stefan-Boltzmann constant (SBC): Forcing (F) (W/m²) = 5.6705 x 10-8 x K4 At 255°K: F = 5.6705 x 10-8 x (2554) = 239.76 W/m² Dividing radiation by 20: 239.76 W/m² ÷ 20 = 11.988 W/m² Changed SBC: x = F/K4 = 11.988 ÷ (255)4 = 2.8352 x 10-9 Whereby: F = 2.8352 x 10-9 x K4 Adding 3.7 W/m² to 11.988 W/m² = 15.688 W/m² K4 = F/x = 15.688 W/m² ÷ 2.8352 x 10-9 = y, where y-4 = 272.74°K Changed temperature = 272.74°K - 255°K = 17.8°C Changed primary effect: 5.35ln2 = 3.7 W/m² = 17.8°C upon doubling CO2. Claimed primary effect: 5.35ln2 = 3.7 W/m² = 1°C upon doubling CO2. Why start at 255°K? Climatologists have a quirky and erroneous reason for doing so. Without an atmosphere, the earth's temperature average would be 255°K, when applying the SBC, because the sun sends down 235 W/m² of energy, which is supposedly how much radiation matter gives off at 255°K. Presumably, the analysis should start where there are no greenhouse gases. The trouble is, the analysis calculates how much heat is added to the atmosphere at present time, which is said to average 288°K. Such contradictions don't get resolved in the contrivances. If anything real were studied, each point would be non-contradictory. But applying real science to these questions is totally impossible. So contriving each step of the rationalization leaves endless contradictions which cannot be resolved.
Sometimes, the fudge factor (radiative forcing equation) is attributed to Hansen et al, 1988. But that paper says it is located at Hansen et all, 1984. Actually, it is neither; it is at Myhre et al, 1998. Vincent Gray summarizes the history here. Both Hansen et al, 1988, and Hansen et al, 1984, use modeling to determine the increase in heat produced by increases in CO2. The result is given in a range, as all modeling does. Their typical range is 2-4°C increase upon doubling CO2, with numerous variations for hedging upon various effects. Myhre et all, 1998, use radiative transfer analysis for pretended precision, yielding a constant effect rather than a range. In table 3., CO2, numbers state the precise fudge factor as 5.35 ln C/Co. Radiative transfer studies say nothing of heat in the atmosphere. They were designed to show the rate of diminishing absorption as concentration of a gas is increased in a test tube. Such effects could be determined by varying the concentration, but the same can be done through math instead. The math is extremely complex and requires a lot of computer power.
Hansen, J., D. Johnson, A. Lacis, S. Lebedeff, P. Lee, D. Rind, G. Russell, 1981. Climate Impact of Increasing Atmospheric Carbon Dioxide. Science, 23:957-966. Hansen, J., A. Cacis, D. Rind, G. Russell, P. Stone, I. Fung, R. Ruedy, and J. Lerner, 1984. CLIMATE SENSITIVITY: ANALYSIS OF FEEDBACK MECHANISMS. Geophys. Mono. 29:130-163. Hansen, J., I. Fung, A. Llacis, D. Rind, S. Lebedeff, R. Ruedy, G. Russell, and P. Stone, 1988. Global Climate Changes as Forcast by Goddard Institute for Space Studies, Three Dimensional Model. J. Geophys. Res. 93:9341-9364. Ramanathan, V., M.S. Lian, and R.D. Cess, 1979. Increased Atmospheric CO2: Zonal and Seasonal Estimates of the Effect on the Radiation energy Balance and Surface Temperature. J. Geophys. Res. 84:4949-4958. Myhre, G., E.J. Highwood, K.P. Shine, and F. Stordal, 1998. New estimates of radiative forcing due to well mixed greenhouse gases. Geophys. Res. Lett. 25:2715-2718. myhre.pdf Gray, V., 1999. Greenhouse Warming Reduced. Greenhouse Gas Bullitin 121, John-Daly.com IPCC, AR3, 1.3.1, 2001 IPCC, AR3, 6.3.1, 2001 |
 |
||||||||||||||||||||
The main secondary effect is said to be due to water vapor heating when absorbing radiation due to carbon dioxide heating the atmosphere.
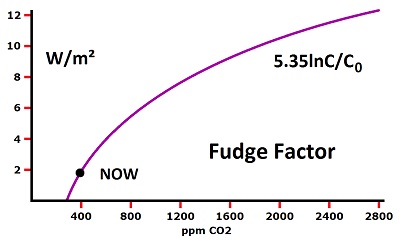
Then where does the 3.7 W/m² enter in? A fake logic goes back and forth between a restricted exit and a reduced emission. And the entire analysis omits the 15-30% radiation which leaves throughout the atmosphere, not at the top, and which does almost all of the cooling of the planet.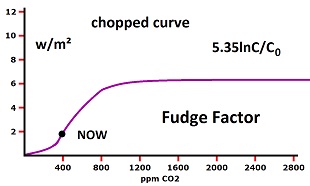
Rationalizers sometimes claim the curve is chopped off outside the desired range, but there is no force in nature to cut it off at the bottom, and only saturation can cut it off at the top. It would have to be an S shaped curve. There are no influences in nature to create such a curve. The claim is total fakery attempting to conceal the absurdity of the fudge factor.
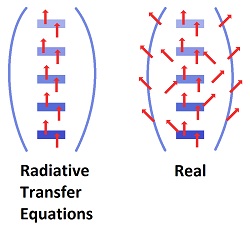Very little radiation does that. Between 15 and 30% of the radiation leaves from the atmosphere, and it does the cooling of the planet.
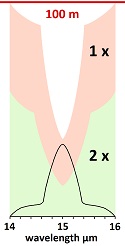He and others concluded that all available radiation is absorbed in 10 meters of travel at the center of the main absorption peak. On the shoulders of the peaks, there are fewer molecules, so more distance is traveled by radiation before being completely absorbed by those molecules.