|
The Cause of Ice Ages and Present Climate |
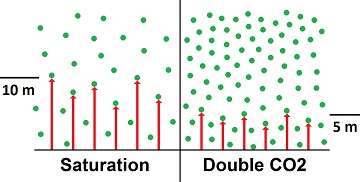
Saturation Carbon dioxide absorbs all radiation available to it in traveling 10 metes in the near surface atmosphere, which is called saturation. Doubling the amount of CO2 shortens the distance to 5 meters. Shortening the distance is not increasing the heat. Climatologists made saturation disappear in calculations called radiative transfer equations. It's not valid to make saturation disappear. Doing so only shows the corruptness of the radiative transfer equations. It's more than strange that climatologists never produced a number for the distance of saturation, though they do admit that saturation exists. Heinz Hug did a laboratory measurement and determined that the saturation distance is 10 meters, but he was not allowed to publish his results. The obvious reason is because there is no global warming with saturation.
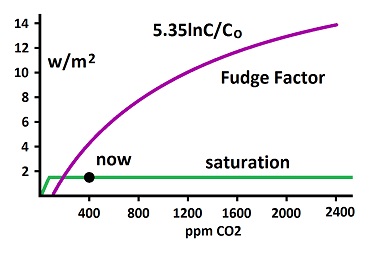
Rationalizers look for a situation represented by the image on the left, where some radiation would go through. At first, they said molecules on the shoulders of the absorption peaks are thin and do what is shown in the image on the left. But that claim would not stand up to criticism; so they switched to the upper atmosphere, where molecules are thinner. The molecules don't get thin enough until they are far beyond the top of the normal atmosphere (troposphere). The insurmountable problem of rationalizers is that when the molecules get thin enough to allow radiation through, they spread the heat so thin that no significant temperature increase can occur. The molecules would have to be one thousandth as dense as at the surface. But that means one thousandths as much temperature change. Heinz Hug showed that only one part per thousand on the edge of the shoulders are relevant to an increase, and this would create a thousand to one ratio for center effect compared to shoulder effect. He stated: "As the transmission T = 10-3.21 is 0.6 per mille, we conclude that the relative absorption around the peak is 1-T = 99.94% which takes place already within a 10 m layer near ground." Radiative Transfer Equations Therefore, scientists eliminated saturation through mathematics without a scientific logic. The basic method of eliminating saturation was to use radiative transfer equations to calculate the amount of radiation that goes through the atmosphere. Saturation is removed in the calculations—no explanation of where it went. The methodology of radiative transfer equations is to slice the atmosphere into numerous small pieces called parcels. The amount of radiation emitted from each parcel is calculate, and the amount of that radiation absorbed into the next parcel up is calculated. This is repeated until the entire atmosphere is covered. The largest computers are used to do this. And what do they have afterwards? Some radiation escaping at the top of the atmosphere, where saturation allows none. Direct measurements easily show the saturation, so obfuscation was needed to erase the saturation. The math for the radiative transfer equations requires a concept of how much radiation is going from each parcel and how much goes into the next parcel. Accounting for saturation must occur to determine these numbers. Therefore, the erasure of saturation occurs in deciding how much radiation goes where. The product of the radiative transfer equations was presented as the fudge factor. In 2001, the IPCC (AR3) stated that saturation exists in these terms:
With this statement there was no explanation of how the shoulder molecules are evaluated for the magical heating, and there was apparently no further mention of shoulder molecules or saturation in subsequent publications of the IPCC reports. Saturation was Reduced to a Trivial Amount With the fudge factor, a small amount of saturation creates the bend in the curve. But the saturation is actually about 10,000 times greater than the fudge factor curve indicates. Measurements, such as that of Heinz Hug, show that the center of the main absorption peak saturates in 10 meters. To get saturation to occur at a height of 10 km would require one thousandth as much saturation. But 10 km is still in the normal atmosphere (troposphere). To get non-saturation of any significance, as indicated by the fudge factor, at least ten times as much distance is required, or one tenth as much saturation, which would be 10,000 times as much as indicated by the fudge factor. To determine the effects of saturation, the question is how far should radiation travel before being totally absorbed. Nowhere in prevailing climatology is there any indication of distance being considered. Implicitly, the radiative transfer equations calculated a series of parcels from the bottom to the top of the troposphere. There is no logic for doing that, since an unfathomable mechanism is usually said to occur at 9 km up, and it is independent of the distance to the earth's surface. But radiation traveling from the surface to the fake mechanism requires at least 9 km to get there. So the distances implied by the radiative transfer equations need to be quite large. The effect of radiative transfer equations is to show that less radiation leaves the atmosphere than enters from the sun, until equilibrium is restored at a warmer temperature for the atmosphere. In doing so, saturation is reduced to trivia, and the mechanism is reduced to simple absorption of radiation throughout the atmosphere, based on the premise that the radiation all starts at ground level and moves upward. Most energy gets into the atmosphere through conduction, convection and evaporation. Therefore, there is no means of determining how far radiation must travel to get out of the atmosphere, which must be known to calculate how much fails to be emitted at the top of the atmosphere.
Why not measure the result in a tube in the laboratory instead of calculate it? The measurement says all radiation is absorbed in 10 meters; the calculation says it is still emitted at 20 km. There can't be a difference. Which is more reliable? The calculation is so infinitely complex that it can't be done. Yet climatologist claim that the resulting fudge factor is an unquestionable principle of physics. What would need to be known to make the calculation is not only all complexities in the atmosphere but the temperature of each parcel, overlapping and interacting radiation waves, which are too numerous and complex to be evaluated, and the amount of radiation being absorbed and emitted by the oceans, which cannot be determined, not the least reason being that the oceans are so heterogeneous with mountains and rivers of temperature variation that surface temperatures cannot be predicted. El Ninos are unpredictable due to the infinite unknowns. This complexity is only necessary because of the claim that the radiation goes through the entire atmosphere when making calculations. The laboratory measurement does not require such complexity, because in 10 meters, there is no significant, atmospheric complexity. Afterwards, converting radiation into temperature is impossible for the same reasons. In addition to the complexities, the temperature will depend upon the amount of time between radiation absorption and re-emission, which is too complex and unknown. |
|||||||||||||||||||||

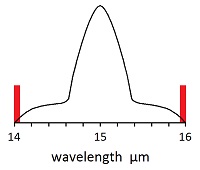
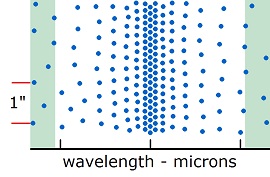
 A gate half open will not keep in half the sheep. The assumption is that equilibrium is created at the top of the atmosphere, but it is created throughout the atmosphere.
A gate half open will not keep in half the sheep. The assumption is that equilibrium is created at the top of the atmosphere, but it is created throughout the atmosphere.