The Stefan-Boltzmann Constant is in Error.

Based on the erroneous Stefan-Boltzmann constant (SBC), a house could be heated by covering the floor with ice. The SBC says 315 watts per square meter of radiation are given off by matter at 0°C (32°F). The emissivity for ice is 0.92. So 0.92 x 315 = 299 w/m².

For a room that is 15 feet by 30 feet, the area can be rounded to 50 square meters. So 50 x 299 = 14,950 watts of radiation being emitted. That's equivalent to 8.3 space heaters at high level of 1,800 watts. That means such a room covered in ice would fry the place in minutes, as if 8.3 space heaters were going.

Reduce the Stefan-Boltzmann constant by a factor of 40, where it should be, and the result would be one fortieth as much atmospheric heating calculated by physicists.

That's why power mongers destroyed the information super highway and replaced it with social media. They have endless frauds to hide. Greenhouse gases would be viewed as a joke, if people knew how little radiation is available for carbon dioxide to absorb.

The Stefan-Boltzmann constant states the amount of radiation emitted by matter (watts per square meter) at any particular temperature. It's about 40 times too high at normal temperatures.

A corrected amount of radiation would show there to be one fortieth as much radiation available to carbon dioxide in the atmosphere as physicists claim.

With the Stefan-Boltzmann constant being excessively high, an extremely large amount of radiation from the surface of the Earth is available to be absorbed by carbon dioxide in the atmosphere. Reduce the radiation, and the greenhouse effect is a joke.

The Stefan-Boltzmann constant says that matter emits 459 watts per square meter of infrared radiation at the normal room temperature of 27°C. That's one half of a table top emitting as much energy as five 100 watt light bulbs. Nothing resembling it is happening. Ice supposedly radiates 315 W/m². That's three 100 watt light bulbs per square meter of ice. You could heat a room with a few square meters of ice. Reduce the Stefan-Boltzmann constant by a factor of 40, and the calculated global warming reduces by a factor of 40.

radiation

The Stefan-Boltzmann constant shows how much radiation is given off by a square meter of any substance at a particular temperature. It is inappropriately applied to the atmosphere where there is no surface and where a transparent gas emits radiation much more readily than a surface does.

W/m² = 5.670373 x 10^-8 x K⁴

Watts per square meter radiation equals a constant times degrees Kelvin to the fourth power.

Simple observations indicate that 20-50 times too much radiation is projected by the Stefan-Boltzmann constant at normal temperatures. The accuracy at higher temperatures is not apparent. The actual curve would be different for each type of molecule. Straight lines should exist between changes in molecular states.

An indication of the error is in the global energy budget which climatologists use. They have to show 79% of the energy leaving the surface of the earth is in the form of radiation because of the Stefan-Boltzmann constant. (See the NASA Energy Budget) A white hot light bulb could not emit 79% radiation without a vacuum environment. Climatologists know that number is preposterous, but it is locked into a narrow range by the Stefan-Boltzmann constant. The actual amount should be 1-3% (estimated maximum). Representing that amount as 2%, in means the Stefan-Boltzmann constant is too high by a factor of 40.

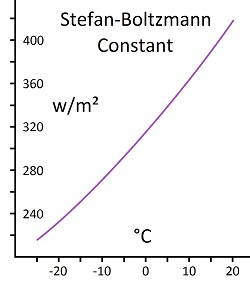
The 1-3% is my estimate of a maximum possibility having worked extensively with temperature effects in electronics; but only a maximum possibility can be estimated through elimination, while the actual would be much less. Radiation is so minuscule that it is ignored in most heat analysis, which means it could not be more than 1-3% of heat loss, while the actual would be much less but cannot be estimated at such a low level. Physicists have not determined what the number should be, which is why they could produce the absurd 79%.

The Stefan-Boltzmann constant is this:

W/m² = 5.670373 x 10^-8 x K⁴

This result is the number of watts per square meter of infrared radiation supposedly given off by matter at a temperature represented by K (degrees Kelvin, which is 273 + °C).

For exactness, this calculation must be adjusted for emissivity, which means variation from the Stefan-Boltzmann constant. For rough, nonreflective materials, it is usually in the range of 75-95%. These variations show the influence of chemistry.

At a normal temperature of 27°C (80°F), the Stefan-Boltzmann constant without emissivity indicates 459 W/m² being radiated.

At the assumed average temperature of the earth (15°C, 59°F), it's 390 W/m².

At the freezing temperature of water (0°C, 32°F), it's 315 W/m².

On a hot day of 37°C (98°F), it's 524 W/m².

On a real cold day of -23°C (-10°F), it's 221 W/m².

It isn't happening. Normal temperature matter is not giving off that much infrared radiation. Virtually everything in physics is in error, unless someone gets the error corrected, which requires a lot more accountability than often exists.

If freezing water were emitting and absorbing the heat of three 100 watt light bulbs per square meter, the heat would interfere with the freezing process. Freezing would be highly finicky and prone to variation.

Physicists have an answer. They say the same amount of radiation is being emitted as absorbed at a stable temperature, so you don't notice the difference. No way. If skin cells were giving off and absorbing 524 W/m² at 98°F, tissue damage would occur between absorption and emission. Energy gets moved around by conduction between absorption and emission of radiation.

Warm clothes would not be warm, if radiation were such a high rate. The insulating effect is largely air space. Air space would be irrelevant at such a high level of radiation. Eskimos use very loose clothes, so a lot of warm air accumulates in them. Warm air would be ineffective if there were a lot of radiation going outward at 524 W/m² and a lot less radiation going inward at 221 W/m² (-23°C).

For example, all electronic components are evaluated for heat to make sure they won't over-heat. Without a fan or air currents for significant convection, which means mostly radiation, almost no cooling occurs. Radiation is in the 1-3% range for warm objects which are cooling by normal convection into the air and closer to zero percent with some air movement such as the constant wind over the surface of the earth.

Yet, climatologists claim radiation is 79% of the heat dissipation from the surface of the earth, which is a cold 15°C average with wind equivalent of a fan blowing.

Not the least reason for the error is that Planck's constant is used to derive the SBC, while there is no Planck's constant, because the whole concept of photons is absurd and admittedly in conflict with the wave nature of light.

The errors in the Stefan-Boltzmann constant are used to rationalize greenhouse gases.

Background Science: Heat causes molecules to vibrate. The vibration of the nuclei sends infrared radiation outward at the same frequency that the nuclei vibrate. More heat creates higher frequency vibrations and higher frequency infrared radiation. Heat also increases the intensity of the radiation.

The Stefan-Boltzmann constant deals with the amount of radiation emitted. With an opaque solid, only the surface molecules emit radiation. Radiation cannot escape from within. That's what opaque means. But a transparent gas such as the atmosphere will obviously allow radiation to escape from within it.
This is why infrared cameras show the atmosphere glowing at night, while solids are black. The depth of the atmosphere allows much more radiation to be emitted than does the surface of solids.

Physicists wrote an equation for the relationship between temperature and the amount of radiation emitted from a surface. Now they apply it to radiation from the atmosphere, which does not have a surface. Square meters are interchanged with cubic meters.

They apply it to all matter—solids and gasses—at all temperatures. It is not logical that radiation would be uninfluenced by molecular forces including bonding and molecular weight. The absurdity of the result at normal temperatures shows that the equation does not properly represent nature.

Anyone would know that radiation will escape from a transparent gas immensely easier than from an opaque solid. Applying the Stefan-Boltzmann constant to the atmosphere says the emission is the same for the atmosphere as for a solid surface. The only reason it is being done is because climatology cannot be reduced to simple math without the Stefan-Boltzmann constant.

Do you think physicists measured the different substances to determine whether they all emit the same? They wrote up a ridiculously simplified equation and applied it to everything. It's a convenience equation. And it's not science. Physicists operate on the engineering principle that if they all use the same twisted ruler, it doesn't matter; and therefore, ultra simplification is called for. In science it matters.

In engineering, it's valid to reduce math to its simplest form; in science, it's not. Yet physicists do; and they reduce physics to engineering in the process. When the basics of physics were being formulated into mathematical equations, about a century ago, the gods of physics had not the slightest ability to evaluate the complexities of the subject, yet they wrote math equations to represent complex phenomena as if nature could be reduced to such simplicity. Their equations are not valid for the complexities of nature. With the Stefan-Boltzmann constant, the reality is that every molecular difference would produce a different constant, yet only one constant is used for all conditions. Engineering thrives on such simplifications, but science is reduced to fraud by it.

Here's the problem with the Stefan-Boltzmann constant: Satellite measurements indicate that the sun's energy approaching the earth is 1366 watts per square meter. The amount reflected away is said to be 26%. The amount absorbed into the atmosphere is said to be 16%. (See NASA chart). That's 1366 minus 26% minus 16% = 792 W/m². That's how much radiation would fall on a black asphalt surface at the equator at noon. The Stefan-Boltzmann constant indicates that in a dark basement, a concrete wall at 59°F (the global average temperature) would emit 390 W/m². That's 49% as much radiation emitted from a dark, cold basement as falls on a black surface at the equator. It isn't happening.

Night vision equipment shows that there is very little infrared radiation given off by normal temperature matter.

You have to realize that physicists pull their equations out of thin air and adapt them to a purpose, usually to expedite technology. It's not a scientific process. Their math is always too simplistic to represent the complexities of nature.

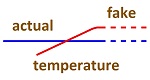
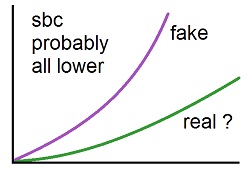
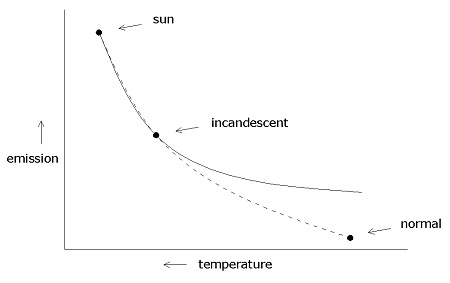
Fake Curve

On the graph below, the solid line is the curve produced by the Stefan-Boltzmann constant. The dotted line shows that there needs to be less radiation given off by normal temperature matter. The difference is the error in the Stefan-Boltzmann constant.

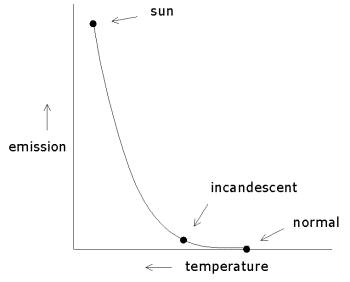
Supposedly, the sun gives off 63 million W/m² at 5,780°K; an incandescent bulb, 4.6 million W/m² at 3,000°K; and normal matter, 459 W/m² at 300°K.

To scale, the Stefan-Boltzmann curve looks like this:

The fourth power on temperature creates an extreme bend in the curve and causes it to go almost straight horizontal at normal temperatures. The horizontal area shows way too much radiation at normal temperatures. The excessive radiation at normal temperatures is used to rationalize greenhouse gases.

Natural effects do not normally have high exponents. The fourth power is probably a result of two errors combined—a squared result (exponent of 2) in heat and temperature relationships, which are assumed to be linear (nonexponential) and a squared result for heat and radiation relationships. But there would not be one curve for heat-radiation relationships. Chemistry and other forces would create too much variation for a single curve, as indicated by emissivity. At extreme temperatures, additional forces probably add more variations.

The linear relationship between heat and temperature is a convenience assumption based upon a closed circle of logic, because the actual measurements are extremely difficult to make and are not realistically being made. The transformation of kinetic energy into heat is represented by Joule's constant, which is given to 5 significant digits. But I showed mathematical proof that the definition of kinetic energy is wrong, which means there is no consistent Joule's constant. The 5 digit number has to be fakery.

The actual curve for heat and radiation relationships looks like it would be S shaped, because a lot of change would occur at normal temperatures. Physicists used a smooth curve resulting from a simple exponent, and as a result, they got too much radiation at normal temperatures.

Due to the exponent of 4 in the Stefan-Boltzmann constant, physicists have 11 times as much radiation being given off by the sun as a light bulb filament but only 1.9 times as much temperature. There could be other forces entering at the temperature of the sun, but this would be a bend in the curve, not an exponential curve. Is twice the temperature of a light bulb filament supposed to produce hydrogen fusion? Not hardly.

The Atmosphere Supposedly adds 33C to the Earth's Surface.

There is an average of 235 W/m2 energy leaving the earth. The Stefan-Boltzmann constant says that an object at -19°C emits 235 W/m2 black body radiation. But the average earth surface temperature is 15°C. So the earth's surface is 15 + 19 = 34 (rounded to 33) degrees C warmer than it would be without an atmosphere. The atmosphere supposedly keeps the earth's surface warm.

In truth, greenhouse gasses add no heat to the atmosphere, because heat as radiation cools the planet by going around them, not through them. The atmosphere does not need greenhouse gasses to absorb and hold heat, as explained on the page titled Summary in Simple Words.

With a corrected Stefan-Boltzmann constant, the surface of the earth without an atmosphere would emit 235 W/m² at a temperature of something like 50°C, not -19°C. With an atmosphere, the surface average is 15°C. The atmosphere cools, as it should, because it is like a heat sink. This means the atmosphere picks up energy through conduction and convection, which removes heat much faster than radiation alone. Heat sinks (usually made of aluminum) are used for this reason throughout electronics to speed cooling.

Theoretical Concepts

Physicists do not do conception analysis. They despise intuitive logic. Instead, they apply math without regard for the resulting absurdities. The problem is that the math has a high tendency to be wrong, incomplete or over-simplified.

Besides the Stefan-Boltzmann constant resulting in too high of a quantity at low temperatures, the constant is applied to solids and gasses equally, which is absurd. Gasses have a three dimensional surface and low density, which promote the escape of radiation. Therefore, gasses should have a much higher quantity for radiation emission than solids. But there would not be a single constant for gasses, because the chemical composition would determine how radiation escapes, as greenhouse gasses demonstrate.

These points should be quite secondary and not much relevance to global warming, because other factors determine the result. But fake scientists rely heavily upon the Stefan-Boltzmann constant as a rationalization gimmick. They focus upon such claims as radiation leaving the earth at a height of 5km attempting to create a concept in minds of there being a greenhouse effect. Global warming propaganda is all about impressions and a dark pit of unaccountable rationalizations.

Errors in Physics

Why is the Stefan-Boltzmann constant so far off? Observable evidence shows that errors in science, particularly physics, are the maximum which accountability will allow. In physics, there is far less accountability than in biology due to its highly abstract nature.

Consider this simple example. Physicists claim that the Bernoulli principle shows that the pressure of a gas is inversely proportional to velocity, and this allows airplane wings to lift weight due to the high velocity of the air over the top. The velocity is lower under the wing due to less curvature and less distance to travel. You can prove the physicists wrong by blowing on one side of a sheet of paper. Nothing happens. But fold a crease in the paper, and then blow across it. The paper is rapidly pulled by the crease. The crease creates a vacuum pump in the shaded area. High velocity air pulls air molecules out of a shaded area creating a vacuum pump. It is not the velocity alone but the shaded area that creates the force. This means physical shape, not raw velocity, determines the pressure effects of moving air, contrary to the claims of physicists.

This is why an airplane wing needs its bulge near the front instead of the back. If it were raw velocity creating the lift, the bulge would need to be near the back of the wing to increase the surface over which the high velocity air travels. But if it is a vacuum pump creating the lift, the bulge needs to be near the front, so there is more area for the vacuum behind the bulge. The wings have the bulge in front showing that it is the vacuum behind the bulge, not the high velocity in front of the bulge, which does the lifting.

TOP