|
| Gary Novak
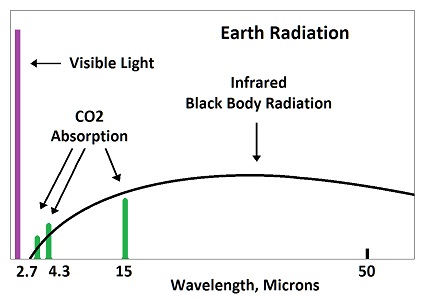
The Cause of Ice Ages and Present Climate |
It's extremely strange that radiation was calculated, when there is no method of converting radiation into temperature. The radiation was calculated using radiative transfer equations with the results expressed as the three component fudge factor. From this, the primary effect of carbon dioxide heating the atmosphere is supposedly determined.
To model temperature increase due to CO2, a primary effect is the starting point, and then secondary (feedback) effects are added. The primary effect is described as "radiative forcing due to CO2 without feedback," which is the fudge factor, and this is converted to a temperature with a "conversion factor." The result is said to be 1°C for doubling CO2 in the atmosphere. The simple math is this: Primary Effect (Fudge Factor) The fudge factor is, 5.35 times the natural log of the increase in CO2, which is 2 for doubling CO2. It yields 3.708 W/m² upon doubling CO2 in the atmosphere. Getting 1°C is a mystery which is revealed by applying the Stefan-Boltzmann constant as shown below. The fudge factor is promoted as an unquestionable law of physics upon which all else in global warming is based. It is the primary effect from which secondary effects are modeled. Only the secondary effects are in question. The calculation is total fakery. While conservatives oppose the concept of global warming, they claim the calculation of the primary effect through radiative transfer equations is flawless physics, while global warming is not occurring because of clouds. It shows that conservatives are not producing a better analysis but trying to protect another power structure by pretending that physics is flawless science. What this means is that climatologists claim that the primary effect upon doubling carbon dioxide in the atmosphere will heat the atmosphere by 1°C, and then modeling is used to determine secondary effects, which supposedly add 2°C for a total of about 3°C. The primary effect is not questioned, supposedly being an absolute law of physics, and only the secondary effects are studied and argued. A source for this claimed law of physics cannot be determined. A quote for it comes from Stefan Rahmstorf, "Anthropogenic Climate Change: Revisiting the Facts." P34-53 in "Global Warming: Looking Beyond Kyoto," by Ernesto Zedillo. 2008, where he said this: "Without any feedbacks, a doubling of CO2 (which amounts to a forcing of 3.7 W/m²) would result in 1°C global warming, which is easy to calculate and is undisputed." Rahmstorf's citation is this: "IPCC, Climate Change 2001: Synthesis Report." There is nothing resembling the Rahmstorf claim in the IPCC reports. Inquiring scientists cannot find a source for the calculation which Rahmstorf refers to. Attempts to explain it result in endless complexity and confusion. The simple reason is because there is no way to determine temperature from radiation in the atmosphere.
Climatologists use the Stefan-Boltzmann constant (SBC) to derive the temperature of 1°C from the 3.7 watts per square meter, because only the SBC shows a relationship between radiation and temperature. Physicists claim the relationships go both ways— from temperature to radiation, and from radiation to temperature. But reversing the SBC is not valid for the atmosphere, because it only applies to surfaces. Radiation is emitted much more readily from a transparent gas than from an opaque solid. The SBC is this: W/m² = 5.670373 x 10-8 x K4 The global average, near-surface temperature is said to be 15°C. Average emissivity is said to be 0.64.
3.708/3.486 = 1.064°C The number 3.708 represents watts per square meter for doubling the amount of CO2 in the air as calculated from the three component summary of the radiative transfer equations, which I call the fudge factor. Therefore, doubling the CO2 supposedly creates the same number of W/m² as a 1°C temperature increase, which is 3.7 W/m². The result is the desired 1°C for the primary effect of doubling CO2 in the atmosphere, as if climatologists could calculate such things with extreme precision. They claim about 1% error on this factor. However, the SBC shows about 20 times too much radiation at normal temperatures. (later evidence indicates the SBC is 40 times too high, not 20 times.) Reducing the radiation in the SBC by a factor of 20 shows this:
3.708/0.175 = 21.189°C The result shows 20 times as much temperature increase as climatologists claim, when the SBC is corrected for too much radiation. None of these results are real, as the claimed radiation (3.708 W/m² upon doubling CO2) was contrived for the purpose of eliminating the significance of saturation. With saturation, no radiation change would occur to increase temperatures as global warming. In addition to the quantitative absurdities, it is not valid to reverse the Stefan-Boltzmann constant as a method of determining temperature, and there is no other method of getting temperature out of any scientific calculation. Temperature is determined by the total energy dynamics of changing systems, with heterogeneity in complex systems. The forward direction of the SBC looks only at a definable surface, while the reverse of the SBC is influenced by the total dynamics. Yet the result of the radiative transfer equations is translated into the temperature of the near-surface atmosphere based upon a claimed reduction in emission at the top of the troposphere. What this shows is that climatologists started at the end point of 1°C being the desired near-surface temperature increase upon doubling CO2 in the atmosphere, but correcting the math (SBC) shows 20 times more than they would have wanted for a result.
So, how real is the error in the Stefan-Boltzmann constant? Saying that a cold basement wall at 15°C is giving off 390 w/m² is totally preposterous. Physicists are not exactly saying otherwise, they are saying that it also absorbs that amount, so you do not notice anything. But that claim is absurd also, because biological process, and other complexities such as ice melting, would be sensitive to the difference between emission and absorption, and skin cells would be fried by that much energy being absorbed, regardless of how or when it is re-emitted. Before absorbed radiation can be re-emitted, it must first be converted into heat, which means molecules vibrating. Those vibrating molecules increase in their chemical reactivity as their temperature increases. Biological systems will not tolerate significant increases in temperature without being destroyed. Biology is like a thermometer which can tell the difference between radiation absorption and emission. If a cold basement wall were emitting 390 w/m², you wouldn't be able to get near it without skin cells being rapidly heated and damaged. It means there is no mysterious cancellation of the high absorption and emission indicated by the SBC, and it means climatologists started at a desired end point and contrived the method of getting there. It's the only thing they do in climatology, because the randomness and complexities of climate cannot be reduced to scientific analysis. Another problem with such an analysis is that the SBC is not appropriate for the purpose. It relates to the surface of an opaque solid. But the temperature in question is the near-surface air temperature. A transparent gas radiates in a vastly different manner than the surface of an opaque solid. The absurdity of the Stefan-Boltzman constant shows up in an extreme way in the attempts to create an energy flow chart for the planet, described here.
This image shows how energy is re-distributed when radiation is absorbed by carbon dioxide. 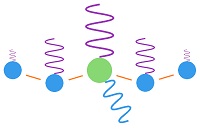 When a molecule of CO2 in the atmosphere absorbs fingerprint radiation (the only thing in question) it increases in vibratory motion, which is heat. As it bumps into surrounding molecules (mostly nitrogen gas), it imparts some motion, which reduces its own motion, while increasing the motion of the other molecule. The vibrating motion of molecules sends out waves of infrared radiation. As the molecular motion decreases, the intensity of the radiation and its frequency get lower. The amount of such bumping and re-emitting that must occur to lose the energy gained by absorption depends upon how strong the radiation is that is absorbed, which is determined by the temperature of the emitting molecules. Emissions from the surface of the earth into the atmosphere would go from warmer to colder. For short distances in the atmosphere, the emitting temperature would be about the same as the absorbing temperature.
Absorbed radiation (fingerprint radiation) is weaker than emitted radiation (black body radiation), because 8% of black body radiation is fingerprint radiation absorbed by CO2. In the above image, 8% of the horizontal distance is CO2, as tested during the early fifties. A small amount of energy would be spread to nearby molcules before being radiated away. A CO2 molecule would lose about half of its gained energy in one half cycle as it bumped a nearby molecule (usually nitrogen). It would then impart half of its excess energy into the molecule it bumps. One half of one half equals one fourth of the increased energy being imparted into the bumped molecule. The bumped molecule would do the same thing and impart one fourth of its added energy into the molecule which it bumps. This means that three fourth of the energy picked up by CO2 is radiated away, while one fourth if added to nearby molecules. The energy cannot spread significantly before being radiated away by a small number of molecules. This is why there is no such thing as trapping heat in the atmosphere. Where then do the 3.7 watts per square meter come from? They are the difference between the amount of radiation assumed to go into space based on the calculations of the radiative transfer equations and the amount entering the earth from the sun. Who cares where or how that difference in radiation creates heat. It has to create heat someplace. One of the problems is that the calculations are not direct enough to do a comparison between calculated radiation at the top of the atmosphere and the total energy entering from the sun. The differences are extreme and render all such analysis so absurd that any result has to be a predetermined contrivance.
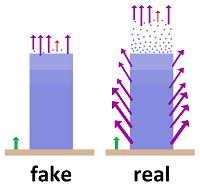
The NASA energy budget claims 41% of the heat on the surface of the earth leaves as radiation. It's a preposterous guess. Only white hot metals give off 41% of their energy as radiation. Cooling fans would never be used if that much radiation were emitted from a cold and rough surface with wind blowing over it. The real number would be closer to 1-3% on land, very little from oceans. The Kiehl-Trenberth model shows 79%. That model is forced into a ridiculously high number, because the Stefan-Boltzmann constant was applied, and it is in error. There is about a 100% difference between these two official sources. How reliable can the radiative transfer equations be in picking some such starting point? But the problem is even worse due to the fact that very little of the radiation in the atmosphere gets there by radiating from the surface of the earth. Most heat gets into the atmosphere through conduction, convection and evaporation from the surface, and quite a bit from solar energy. Kiehl-Trenberth says 29% of the solar energy enters the atmosphere rather than striking the earth's surface. The NASA model says 19%. Much of the energy in the atmosphere is converted into radiation, as all matter emits radiation in proportion to its temperature. How fast the transformation of energy occurs is anyone's guess. In other words, the application of radiative transfer equations involves no ability to determine how much radiation is coming from where or going to where. And yet the equations are portrayed as being so precise in their latest rendition that they could determine that earlier calculations were only off by 15%. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||

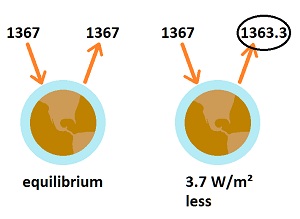
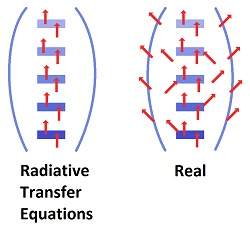 There is nothing resembling a starting point for such an analysis. No radiation or heat on planet earth has an identifiable or quantifiable starting piont other than the total entering from the sun. Implicitly, the radiation at the starting point is that which is emitted from the surface of the earth. No one has a clue as to what that quantity would be, and it is almost irrelevant to the process.
There is nothing resembling a starting point for such an analysis. No radiation or heat on planet earth has an identifiable or quantifiable starting piont other than the total entering from the sun. Implicitly, the radiation at the starting point is that which is emitted from the surface of the earth. No one has a clue as to what that quantity would be, and it is almost irrelevant to the process.